Содержание
Округление чисел бесплатный онлайн калькулятор
Если вы ищете простой способ округлить дробное число, онлайн-калькулятор может значительно упростить эту задачу. С помощью этого инструмента вы можете быстро округлить десятичные числа до целых, цифр, десятков, сотен или тысяч. Это исключает любые догадки и экономит время при работе с большими числами. Кроме того, он бесплатен и прост в использовании — просто введите желаемое значение и установите соответствующие параметры для округления. Независимо от того, какой тип округления вам необходим, этот онлайн-калькулятор справится с этой задачей!
Инструкция по использованию калькулятора
Инструкция калькулятора округления чисел
Калькулятор округления чисел позволяет вам быстро и легко округлить дробное число до нужного разряда, например, до целого, десятков, сотых или тысячных. Чтобы использовать этот калькулятор, следуйте простым инструкциям:
Введите дробное число, которое вы хотите округлить, в поле «Введите число».

Выберите нужное вам округление в поле «Округлить до». Вы можете выбрать округление до целого, десятков, сотых или тысячных.
Нажмите кнопку «Округлить».
Результат округления отобразится в поле «Результат».
Обратите внимание, что в поле «Результат» отображается округленное число с двумя знаками после запятой.
Кроме того, если вы используете мобильный телефон или настольный компьютер, калькулятор имеет адаптивный дизайн и будет работать и выглядеть хорошо на любом устройстве.
Примеры округления чисел на этом калькуляторе
Примеры округления чисел
Калькулятор округления чисел позволяет округлять дробные числа до определенного разряда, в зависимости от выбранного значения в поле «Округлить до».
Примеры:
- Округлить число 7,8531 до целого — результат будет 8.
- Округлить число 12,389 до десятков — результат будет 12,4.

- Округлить число 3,426 до сотых — результат будет 3,43.
- Округлить число 0,03421 до тысячных — результат будет 0,034.
Для округления числа нужно ввести его в поле «Введите число», выбрать разряд, до которого нужно округлить, в поле «Округлить до» и нажать кнопку «Округлить». Результат округления будет отображен в поле «Результат».
Как округлит число до сотых 8491,5372 на этом калькуляторе
Округление числа до сотых 8491,5372
Для округления числа до сотых на этом калькуляторе, следуйте этим шагам:
Введите число, которое вы хотите округлить в поле «Введите число». В этом случае, введите 8491.5372.
Выберите «Округлить до» на «сотых» в выпадающем меню.
Нажмите кнопку «Округлить».
В поле «Результат» будет показано округленное число, которое в данном случае будет равно 8491.54.
Таким образом, чтобы округлить 8491,5372 до сотых на этом калькуляторе, вам нужно ввести 8491.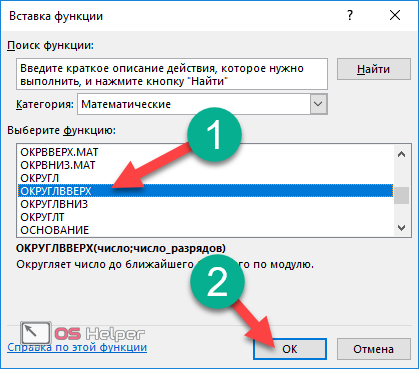 5372, выбрать «Округлить до» на «сотых» и нажать «Округлить».
5372, выбрать «Округлить до» на «сотых» и нажать «Округлить».
Кому будет полезен этот калькулятор
Этот калькулятор будет полезен
Этот калькулятор округления чисел может быть полезен людям, которые работают с числами и нуждаются в быстром и точном округлении до определенных разрядов. Он может быть полезен для бухгалтеров, финансистов, математиков, статистиков и всех, кто занимается расчетами и анализом данных. Также калькулятор может быть полезен для обычных людей в бытовых ситуациях, когда нужно быстро округлить сумму денег или результаты измерений.
В каких ситуациях его можно использовать и чем он поможет
Чем он поможет
Этот калькулятор округления чисел может быть полезен в различных ситуациях, например:
В финансовых расчетах, где необходимо округлить суммы до определенного числа десятичных разрядов.

В научных и инженерных расчетах, где требуется проводить округление результатов измерений, чтобы избежать излишней точности и ошибок округления.
В коммерческих расчетах, например при расчете цен на товары, где цены могут быть округлены до определенных десятичных разрядов.
В повседневной жизни, например при подсчете скидки на товар или расчете процентов по кредиту.
Калькулятор поможет быстро и точно произвести необходимое округление чисел и избежать ошибок при ручном округлении.
Правило округление чисел
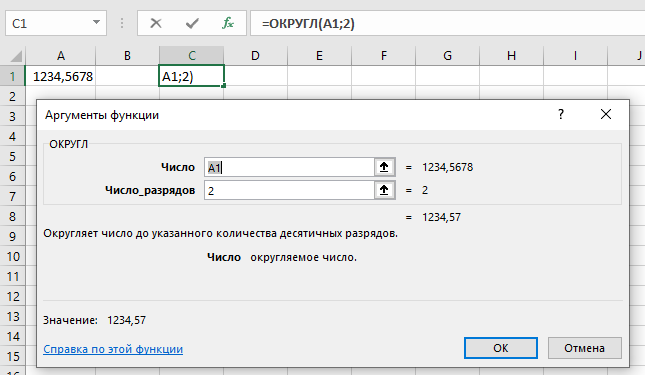
Правило округления чисел зависит от того, до какого знака после запятой нужно округлить. В общем случае, если цифра, которая стоит сразу после той, до которой мы округляем, меньше пяти, то предыдущая цифра не меняется. Если эта цифра больше или равна пяти, то предыдущая цифра увеличивается на единицу.
Например, если мы хотим округлить число 3,4567 до двух знаков после запятой (до сотых), то смотрим на третью цифру после запятой (6), которая больше пяти, поэтому вторая цифра после запятой увеличивается на единицу и получаем ответ 3,46.
Если третья цифра после запятой была меньше пяти, то вторая цифра осталась бы неизменной, и ответ был бы 3,45.
Округление отрицательных чисел
Правило округления отрицательных чисел такое же, как и для положительных чисел, однако нужно учитывать знак числа. Если дробное отрицательное число округляется до ближайшего целого, то сначала применяется правило обычного округления, а затем меняется знак полученного целого числа. Например, если нужно округлить число -1.75 до ближайшего целого, то сначала мы округляем 1.75 до 2, а затем меняем знак и получаем -2. Если же число -1.25 округляется до ближайшего целого, то мы сначала округляем 1.25 до 1, а затем меняем знак и получаем -1.
Виды округления чисел
Существует несколько видов округления чисел:
Округление до ближайшего целого числа (обычное округление) Это самый распространенный вид округления.
 При этом числа с дробной частью от 0,5 до 0,999 округляются до следующего целого числа, а числа от 0 до 0,499 округляются до предыдущего целого числа.
При этом числа с дробной частью от 0,5 до 0,999 округляются до следующего целого числа, а числа от 0 до 0,499 округляются до предыдущего целого числа.Округление до ближайшего четного или нечетного числа (банковское округление) Этот вид округления применяется в банковском деле. При округлении до ближайшего четного числа, дробные числа от 0,5 до 0,999 округляются до ближайшего четного целого числа, а от 0 до 0,499 – до ближайшего нечетного целого числа. При округлении до ближайшего нечетного числа, дробные числа от 0,5 до 0,999 округляются до ближайшего нечетного целого числа, а от 0 до 0,499 – до ближайшего четного целого числа.
Округление до заданного числа знаков после запятой При этом виде округления, задается количество знаков после запятой до которых необходимо округлить число. Если следующий знак после указанного количества знаков больше или равен 5, то число увеличивается на 1 в последнем знаке, в противном случае число не изменяется.
Округление до заданного разряда Этот вид округления предусматривает округление числа до заданного разряда (сотен, тысяч и т.
 д.). В этом случае последние разряды отбрасываются, а предыдущий разряд увеличивается на 1, если отброшенная цифра больше или равна 5.
д.). В этом случае последние разряды отбрасываются, а предыдущий разряд увеличивается на 1, если отброшенная цифра больше или равна 5.
Какой вид округления использовать, зависит от конкретной ситуации и требований к точности.
Округление чисел объяснение
Округление чисел — это процесс приведения дробного числа к ближайшему целому числу или к числу с заданным количеством знаков после запятой (до определенного разряда). Округление может быть выполнено в большую или меньшую сторону, в зависимости от выбранного метода округления.
Существует несколько методов округления чисел:
Метод математического округления — при округлении число 0,5 округляется в большую сторону, остальные числа до 0,5 округляются в меньшую сторону. Например, число 3,5 будет округлено до 4, а число 3,4 — до 3.
Метод округления в меньшую сторону — все дробные числа отбрасываются.
 Например, число 3,9 округляется до 3.
Например, число 3,9 округляется до 3.Метод округления в большую сторону — все дробные числа округляются в большую сторону. Например, число 3,1 округляется до 4.
Метод банковского округления — это специальный метод округления, который используется в банковской сфере. Он заключается в том, что число округляется до ближайшего четного числа, если число после запятой равно 0,5. Например, число 3,5 округляется до 4, а число 4,5 — до 4.
Правила округления могут также зависеть от того, какое количество знаков после запятой должно быть оставлено. Например, если число должно быть округлено до двух знаков после запятой, то число 3,456 будет округлено до 3,46, а число 3,453 — до 3,45.
Формула округления чисел
Формула округления чисел зависит от того, какое округление используется. Вот формулы для наиболее распространенных методов округления:
Округление до ближайшего целого числа:
Если дробная часть числа меньше 0,5, то число округляется вниз до ближайшего целого числа, а если дробная часть числа больше или равна 0,5, то число округляется вверх до ближайшего целого числа.
 n
nГде Math.round() — функция округления до ближайшего целого числа.
Округление до определенного разряда:
Для округления до определенного разряда (десятки, сотни, тысячи и т.д.) нужно разделить число на нужное значение разряда, округлить до ближайшего целого числа, а затем умножить результат на значение разряда. Формула для округления до определенного разряда:
округленное число = Math.round(число / значение разряда) * значение разряда
Например, для округления до сотен значение разряда будет равно 100.
Арифметическое округление чисел
Арифметическое округление — это метод округления чисел, при котором дробные числа округляются до ближайшего целого числа, при этом если дробная часть равна или больше 0,5, то число округляется в большую сторону, а если дробная часть меньше 0,5, то число округляется в меньшую сторону.
Формула для арифметического округления выглядит следующим образом:
Если дробная часть числа больше или равна 0,5: округленное число = целая часть числа + 1
Если дробная часть числа меньше 0,5: округленное число = целая часть числа
Например, для числа 3,75:
- Дробная часть равна 0,75, что больше или равно 0,5, значит, число округляется в большую сторону: округленное число = 3 + 1 = 4
- Для числа 2,3: дробная часть равна 0,3, что меньше 0,5, значит, число округляется в меньшую сторону: округленное число = 2
Округление дробного числа
Округление дробного числа происходит путем отбрасывания дробной части числа и прибавления 1 к целой части, если первая отброшенная цифра равна или больше 5. Если первая отброшенная цифра меньше 5, то целая часть не изменяется.
Если первая отброшенная цифра меньше 5, то целая часть не изменяется.
Например, чтобы округлить число 3,78 до целого, нужно отбросить дробную часть, и получить число 3. То же самое число, округленное до десятых будет 3,8, так как после отбрасывания второй цифры дробной части, первая отброшенная цифра, 7, больше или равна 5, поэтому к целой части (3) прибавляется 1.
Общая формула округления дробного числа x до целого:
Округление x = int(x + sign(x) * 0,5)
где int() — функция, которая отбрасывает дробную часть числа, sign() — функция, которая возвращает знак числа (+1 для положительных чисел, -1 для отрицательных).
Уважаемые пользователи!
Если вам был полезен наш калькулятор Округление чисел, пожалуйста, оставьте свой комментарий о том, как он помог вам в решении задач, учебе или работе. Ваши отзывы могут быть очень полезными для других пользователей, которые ищут подобный функционал.
Также, если у вас есть какие-либо предложения по улучшению калькулятора или пожелания, связанные с его использованием, пожалуйста, не стесняйтесь оставить свой отзыв. Мы ценим ваше мнение и постараемся учесть все ваши замечания и предложения.
Мы ценим ваше мнение и постараемся учесть все ваши замечания и предложения.
Спасибо за использование нашего калькулятора!
округление и другие действия с числами
Навигация по уроку
- Функция SQL ROUND
- Функция SQL CEILING
- Функция SQL FLOOR
- Другие функции SQL для работы с числами
Связанные темы
- Оператор SELECT
- Агрегатные функции
| Назад | Содержание | Вперёд>>> |
Функция SQL ROUND(результат_вычислений, n) округляет результат вычислений до n-го знака после запятой.
Округление производится по правилам арифметики.
Если n — отрицательное число (−n), то округление происходит до n-го знака перед запятой. Таким образом,
с помощью функции ROUND можно получить и целое число как результат округления.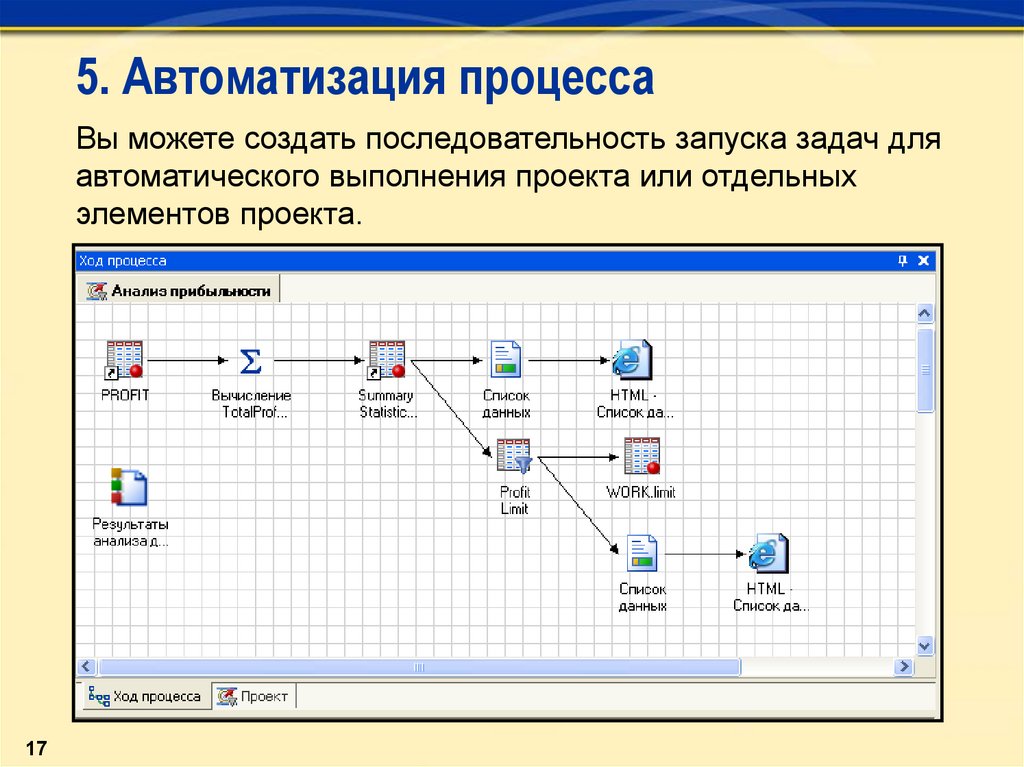
Пример 1. В базе данных фирмы есть таблица Staff, содержащая
данные о сотрудниках фирмы. Выведем индивидуальные размеры заработной платы сотрудников:
SELECT Name, Salary
FROM STAFF
Результатом выполнения запроса будет следующая таблица:
| Name | Salary |
| Sanders | 18357.5 |
| Pernal | 15430.0 |
| Marenghi | 17506.8 |
| Doctor | 12322.8 |
| Factor | 16228.7 |
| Junkers | 16232.8 |
| Moonlight | 21500.6 |
| Aisen | 19540.7 |
| MacGregor | 15790.8 |
Для вычисления среднего размера заработной платы пишем запрос:
SELECT AVG(Salary)
FROM STAFF
Получим следующий результат:
| AVG(Salary) |
| 16990.06662326389 |
Для отчётов результат с таким числом знаков после запятой не годится. Округлим результат до второго
Округлим результат до второго
знака после запятой с помощью функции ROUND:
SELECT ROUND(AVG(Salary),2)
AS Avg_Salary
FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 16990.07 |
- Страница 2. Другие функции SQL для работы с числами
Пример 2. Теперь округлим результат до первого знака до запятой,
применяя в функции ROUND параметр минус единица:
SELECT ROUND(AVG(Salary),−1)
AS Avg_Salary
FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 16990 |
Сместим округление ещё на один знак влево и применим в функции ROUND параметр минус 2:
SELECT ROUND(AVG(Salary),−2)
AS Avg_Salary
FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 17000 |
Функция SQL ROUND может применяться ещё и с третьим необязательными параметром
(кроме MySQL). Если этим параметром будет 1, то округление производиться не будет, просто в результате
Если этим параметром будет 1, то округление производиться не будет, просто в результате
будет оставлено столько знаков после запятой, сколько указано во втором параметре.
Пример 3. Оставить в результате вычислений средней заработной
платы два знака после запятой, не производя округления. Применяем функцию ROUND с тремя параметрами:
SELECT ROUND(AVG(Salary),2,1)
AS Avg_Salary
FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 16990.06 |
- Страница 2. Другие функции SQL для работы с числами
Функция MySQL TRUNCATE
В MySQL аналогом разновидности функции ROUND без округления результата является функция TRUNCATE.
Она, как и ROUND в общем случае имеет два параметра: результат вычислений и число знаков после запятой.
Пример 4. Условие то же, что в примере 3, но в MySQL. Применяем
функцию TRUNCATE:
SELECT TRUNCATE(AVG(Salary),2)
AS Avg_Salary
FROM STAFF
Получим результат без округления, как в предыдущем примере:
| Avg_Salary |
16990.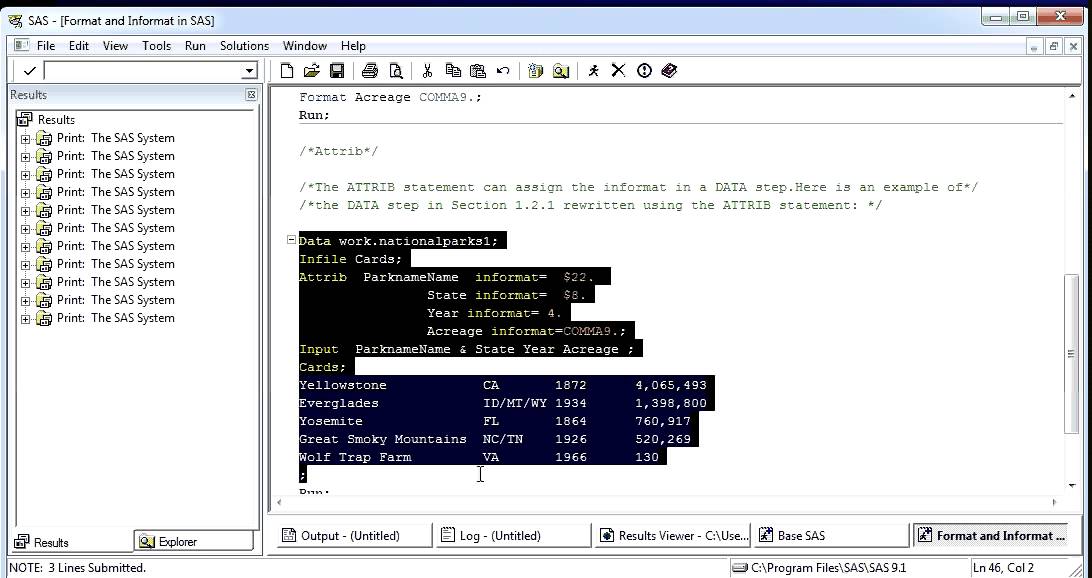 06 06 |
- Страница 2. Другие функции SQL для работы с числами
Функция SQL CEILING не производит округления. Она просто принимает дробное число и возвращает максимальное
целое число, не меньшее принятого. Приведём примеры действия функции с различными принятыми дробными числами.
| Функция с аргументом | Возвращаемое значение |
| CEILING(0.38) | 1 |
| CEILING(1.63) | 2 |
| CEILING(−0.38) | 0 |
| CEILING(−1.63) | −1 |
В случае функции CEILING некорректно говорить об округлении, поскольку она преобразует числа без
учёта правил арифметики.
- Страница 2. Другие функции SQL для работы с числами
Функция FLOOR также не производит округления. Её действие противоположно действию функции CEILING.
Она принимает дробное число и возвращает максимальное
целое число, не большее принятого. Приведём примеры действия функции с различными принятыми дробными числами.
Приведём примеры действия функции с различными принятыми дробными числами.
| Функция с аргументом | Возвращаемое значение |
| FLOOR(0.38) | 0 |
| FLOOR(1.63) | 1 |
| FLOOR(−0.38) | −1 |
| FLOOR(−1.63) | −2 |
Функция FLOOR, как и функция CEILING, преобразует числа без
учёта правил арифметики.
- Страница 2. Другие функции SQL для работы с числами
Поделиться с друзьями
| Назад | Содержание | Вперёд>>> |
6.8 — Форматирование значений данных
Следующая программа SAS иллюстрирует использование оператора FORMAT для указания SAS отображать переменную расход с использованием формата доллара9.2 :
PROC PRINT data = basic LABEL;
имя метки = 'Имя'
клиника = 'Клиника'
расход = 'Расход';
формат счет доллара9. 2;
идентификационное имя;
расходы на вар клинику;
БЕГАТЬ;
2;
идентификационное имя;
расходы на вар клинику;
БЕГАТЬ; | Имя | Поликлиника | Расход |
|---|---|---|
| Элис Смит | ЛЬЮН | 1001,98 $ |
| Мэриэнн Уайт | ЛЬЮН | 2 999,34 $ |
| Томас Джонс | АЛЬТО | 3904,89 $ |
| Бенедиктин Арнольд | АЛЬТО | 1450,23 $ |
| Фелиция Хо | МНМК | 1 209,94 $ |
| Джон Смит | МНМК | 1 763,09 $ |
| Джейн Смайли | МНМК | 3 567,00 $ |
Оператор FORMAT указывает SAS связать на время процедуры PRINT формат Dollar9.2 с переменной Расход . Как только процедура PRINT закрывается, ассоциация больше не сохраняется. Формат доллара 9,2 указывает SAS отображать расходы 9.0004 значения с использованием знаков доллара, запятых (при необходимости) и двух знаков после запятой. 9 сообщает SAS, что для размещения каждого значения расходов потребуется не более 9 пробелов — 1 для знака доллара, 1 для знака запятой, 4 для цифр до запятой, 1 для десятичного знака и 2 для десятичного знака. разместить цифры.
9 сообщает SAS, что для размещения каждого значения расходов потребуется не более 9 пробелов — 1 для знака доллара, 1 для знака запятой, 4 для цифр до запятой, 1 для десятичного знака и 2 для десятичного знака. разместить цифры.
Запустите и запустите программу SAS и просмотрите полученный результат, чтобы убедиться, что значения переменных расхода были напечатаны, как описано. Затем вы можете изменить 9в формате доллара9,2 на 8 и повторно запустите программу SAS, чтобы убедиться, что SAS опускает запятую, чтобы значения помещались в восемь выделенных пробелов. Затем, если вам все еще нравится, вы можете изменить весь формат доллара9,2 на формат запятая8,2 и повторно запустить программу SAS, чтобы ознакомиться с форматом запятой.
Как правило, для каждой переменной можно использовать отдельный оператор FORMAT или можно форматировать несколько переменных в одном операторе FORMAT. В таблице ниже показаны некоторые из наиболее часто используемых форматов SAS:
В таблице ниже показаны некоторые из наиболее часто используемых форматов SAS:
| Формат | Указывает эти значения | Пример |
| ЗАПЯТАЯ w . д | , содержащие запятые и десятичные разряды | запятая8.2 |
| ДОЛЛАР б.д. | , содержащие знаки доллара, запятые и десятичные разряды | доллар 6,2 |
| ММДДГГ w . | как значения даты в форме 03.10.08 ( ммддгг8 .) или 03.10.2008 ( ммддгг10 .) | ммдддгг10. |
| ш . | округляется до ближайшего целого числа в w пробелах | 7. |
| ш.д | округляется до d десятичных знаков в w пробелах | 8,2 |
$ в . | как символьные значения в пробелах w | 12 долларов. |
| ДАТА w . | как значения даты формы 02OCT08 ( date7.) или 02OCT2008 ( date9.) | дата9. |
Конечно, другие доступные форматы можно найти в справке и документации SAS.
Округление
Округление
библиотека (анализ)
Значительная часть проверки связана с округлением. Эта тема более
разнообразны и разнообразны, чем можно было бы подумать. Часто используется «округление».
просто означать округление от 5, и хотя это неправильно, это не
большую часть времени имеют большое значение. Где это имеет значение, так это в
реконструкция процедуры округления, которую использовали другие, утверждают
использовали или предположительно использовали. Короче, округление и все
его детали важны для обнаружения ошибок.
Эта виньетка охватывает инфраструктуру проверки для реконструкции
процедуры округления и результаты сводной статистики. Это
Это
важно для пакета: это предварительное условие для перевода
предположения о процессах, стоящих за опубликованными сводными данными, на несколько
простые вызовы функций более высокого уровня. Некоторые из представленных функций
здесь может быть полезно и за пределами пакета. Не стесняйтесь пропустить
больше теоретических частей, если вы сосредоточены на коде.
Обзор
Функция Base R round() удивительно сложна,
что отличает его от очень простых способов десятичной
числа обычно округляются — в большинстве случаев округление от 5 до 5. Для
однако именно по этой причине его нельзя использовать для восстановления округления
процедур других программ. Это задача наблюдателей
функции округления.
Сначала я представлю reround() , общий интерфейс для
восстановление округленных чисел, прежде чем пройти через отдельные
функции округления. Я добавлю некоторые комментарии к ним.
Я также рассмотрю unround() , который работает в обратном порядке.
способ: принимает округленное число и восстанавливает границы
исходное число с подробностями о предполагаемой процедуре округления
в учетную запись.
Наконец, я более подробно рассмотрю смещение от округления необработанных данных
числа.
Восстановить округленные числа с помощью
reround()
Ни один из методов обнаружения ошибок при проверке не вызывает
отдельные функции округления напрямую. Вместо этого все они звонят
reround() , который является посредником между этими двумя уровнями.
reround() берет вектор «сырых» реконструированных чисел
которые еще не были округлены так, как предполагается,
оригинальная процедура округления. Его следующий аргумент — цифр ,
количество знаков после запятой для округления.
Остальные три аргумента относятся к процедуре округления. Большинство
в то время интерес представляет только , округляя . Это
принимает строку с именем одной из обсуждаемых процедур округления
ниже.
Вот пример вызова reround() :
reround(x = c(5.812, 7.249), цифры = 2, округление = "вверх") #> [1] 5.81 7.25
О двух оставшихся аргументах обычно забывают: они касаются только
непонятные случаи округления с порогом, отличным от 5
( порог ) и округление таким образом, чтобы абсолютные значения
положительные и отрицательные числа одинаковы ( симметричны ).
В противном случае игнорируйте их.
Процедуры округления в деталях
Вверх и вниз
round_up() делает то, что большинство людей считают округлением.
Если десятичная часть, которая должна быть отрезана при округлении, равна 5 или больше, она
округляется. В противном случае оно округляется в меньшую сторону. SAS, SPSS, Stata, Matlab и
Excel использует эту процедуру.
round_up(x = 1,24, цифры = 1) #> [1] 1.2 round_up (x = 1,25, цифры = 1) #> [1] 1.3 round_up(x = 1.25) # по умолчанию для `digits` равно 0 #> [1] 1
Округление до 5 на самом деле является частным случаем
round_up_from() , который может принимать любой числовой порог, не
всего 5:
round_up_from (x = 4,28, цифры = 1, порог = 9) #> [1] 4.2 round_up_from (x = 4,28, цифры = 1, порог = 1) #> [1] 4.3
Эти две функции имеют свои зеркальные отражения в
round_down() и round_down_from() .
аргументы такие же, как и в round_up() :
round_down(x = 1,24, цифры = 1) #> [1] 1.2 round_down(x = 1,25, цифры = 1) #> [1] 1.2 round_down(x = 1.25) # по умолчанию для `digits` равно 0 #> [1] 1
round_down_from() , то это обратная сторона
round_up_from() :
round_down_from (x = 4,28, цифры = 1, порог = 9) #> [1] 4.3 round_down_from (x = 4,28, цифры = 1, порог = 1) #> [1] 4.2
В четное (основание R)
Как в Python round()
функция R base::round() не округляется вверх или вниз, или
использовать любую другую процедуру, основанную исключительно на усеченной части
число. Вместо этого round() пытается округлить до следующего четного
число. Это также называется «банковским округлением».
технический стандарт, IEEE
754.
Понимание того, что round() работает крайне неинтуитивно
иногда приводит в замешательство. Почему мы не можем просто повернуться, как мы
учились в школе, то есть до 5? Причина, похоже, в предвзятости.
Поскольку 5 находится прямо между двумя целыми числами, любая процедура,
раунды 5 в каком-то заданном направлении вносят смещение в сторону этого
направление. Таким образом, округление от 5 смещается в большую сторону, а округление
вниз от 5 смещен вниз.
Как показано в разделе Смещение округления ниже, это
вряд ли будет серьезной проблемой при округлении необработанных чисел, которые изначально
иметь много знаков после запятой. Однако это может быть более серьезно, если
начальное количество десятичных разрядов низкое (по какой-либо причине) и
потребность в точности высока.
По крайней мере теоретически «округление до четного»
направление, и оно сохраняет среднее значение исходного распределения. Что
так работает round() . Вот случай, когда это
Вот случай, когда это
работает, тогда как смещение округления в большую или меньшую сторону полностью
очевидно:
vec1 <- seq(от = 0,5 до = 9,5) up1 <- round_up(vec1) вниз1 <- round_down(vec1) даже1 <- раунд (vec1) vec1 #> [1] 0,5 1,5 2,5 3,5 4,5 5,5 6,5 7,5 8,5 9,5 вверх1 #> [1] 1 2 3 4 5 6 7 8 9 10 вниз1 #> [1] 0 1 2 3 4 5 6 7 8 9 даже1 #> [1] 0 2 2 4 4 6 6 8 8 10 # Исходное среднее значение среднее (vec1) #> [1] 5 # Означает округление в большую или меньшую сторону: смещение! среднее (up1) #> [1] 5.5 среднее (вниз1) #> [1] 4.5 # Среднее значение при округлении до четного: без смещения среднее (четное1) #> [1] 5
Однако эта благородная цель беспристрастного округления наталкивается на
реальность арифметики с плавающей запятой. Таким образом, вы можете получить результаты
из round() , которые на первый взгляд кажутся странными или, по крайней мере,
непредсказуемый. Рассмотрим:
vec2 <- seq (от = 4,5 до = 10,5) up2 <- round_up(vec2) вниз2 <- round_down(vec2) даже2 <- раунд (vec2) vec1 #> [1] 0,5 1,5 2,5 3,5 4,5 5,5 6,5 7,5 8,5 9,5 вверх2 #> [1] 5 6 7 8 9 10 11 вниз2 #> [1] 4 5 6 7 8 9 10 even2 # Здесь нет симметрии... #> [1] 4 6 6 8 8 10 10 среднее (vec2) #> [1] 7.5 среднее (up2) #> [1] 8 среднее (вниз2) #> [1] 7 mean(even2) # ... и среднее немного смещено вниз! #> [1] 7.428571 vec3 <- с( 1,05, 1,15, 1,25, 1,35, 1,45, 1,55, 1,65, 1,75, 1,85, 1,95 ) # Однако здесь нет предвзятости: раунд (vec3, 1) #> [1] 1,0 1,1 1,2 1,4 1,4 1,6 1,6 1,8 1,9 2,0 среднее (vec3) #> [1] 1,5 среднее (раунд (vec3, 1)) #> [1] 1.5
Иногда round() ведет себя как надо, но при
в других случаях результаты трудно объяснить. Мартин Махлер, написавший
текущая версия round() описывает проблему с
следующим образом:
Причина такого поведения заключается в том, что большинство десятичных дробей
на самом деле не могут быть представлены как числа с двойной точностью. Даже
кажущиеся «чистыми» числа с несколькими знаками после запятой
длинная невидимая мантисса и, следовательно, ближе к одной стороне или
другой.
Обычно мы думаем, что все правила округления предназначены для устранения ничьей
это происходит в 5. Однако большинство чисел с плавающей запятой просто
Однако большинство чисел с плавающей запятой просто
несколько меньше или больше 5. Ничьей нет! Следовательно,
Махлер говорит, что функции округления должны «мерить , а не угадывать ».
какой из двух возможных десятичных знаков ближе к x » — и
поэтому, в какую сторону округлить.
Это лучше, чем полагаться на математическую интуицию, которая может
не всегда соответствуют тому, как компьютеры на самом деле справляются с этими
проблемы. R использует настоящее решение, начиная с версии 4.0.0.
base::round() может показаться черным ящиком, но
беспристрастный в долгосрочной перспективе. Я рекомендую использовать round() для
оригинальная работа, хотя она сильно отличается от других округлений
процедуры — и поэтому непригодны для их реконструкции. Вместо,
нам нужно что-то вроде round_*() функций Scrutiny.
Реконструировать границы округления с помощью
unround()
Округление приводит к потере информации. Мантисса обрывается в
Мантисса обрывается в
частично или полностью, а полученное число недоопределено с
по отношению к исходному номеру: последний не может быть выведен из
бывший. Однако может быть интересно вычислить диапазон
исходное число с учетом округленного числа (особенно количество
десятичных разрядов, до которых оно было округлено) и предполагаемое округление
метод.
Хотя часто легко определить такой диапазон, нам лучше иметь
компьютер сделать это. Введите unround() . Он возвращает нижний и
верхние границы, и он говорит, являются ли эти границы включающими или нет —
то, что сильно зависит от процедуры округления. В настоящее время,
unround() используется в качестве помощника при проверке ДЕБЕТ
выполнение; см. виньетку ("дебет") .
Процедура округления по умолчанию для unround() :
"вверх или вниз" :
unround(x = "8.0") #> # Таблица: 1 × 7 #> округление диапазона ниже incl_lower x incl_upper выше #>#> 1 7. 95 <= x(8.0) <= 8.05 up_or_down 7.95 TRUE 8.0 TRUE 8.05
Полный список рекомендуемых процедур округления см.
документация для unround() , раздел Округление .
Слева в столбце диапазона отображается содержательный графический
обзор других столбцов (кроме округления ) в
тот же порядок:
-
ниже— нижняя граница исходного числа. -
incl_lowerравноTRUE, если нижняя граница
включительно иFALSEв противном случае. -
x— это входное значение. -
incl_upperравноTRUE, если верхняя граница
включительно иЛОЖЬиначе. -
верхний— верхняя граница исходного числа.
По умолчанию десятичные разряды подсчитываются внутри, чтобы
функция всегда работает на соответствующем десятичном разряде. Это создает
необходимость учитывать конечные нули, поэтому x
должна быть строкой:
unround(x = "3,50", округление = "вверх") #> # Таблица: 1 × 7 #> округление диапазона ниже incl_lower x incl_upper выше #>#> 1 3,495 <= x(3. 50) < 3.505 up 3.50 TRUE 3.50 FALSE 3.50
Альтернативно, функция, которая использует unround() как
helper может подсчитывать десятичные разряды сам по себе (т. е. путем внутреннего вызова
десятичных_мест() ). Затем он должен передать эти числа в
unround() через аргумент десятичных знаков вместо
позволяя ему избыточно подсчитывать десятичные разряды во второй раз.
В этом случае x может быть числовым, поскольку нули в конце
больше не нужны. (Это, в свою очередь, связано с тем, что ответственность перед
подсчитывать десятичные разряды в числовых строках, а не сдвиги числовых значений
от unround() в функцию более высокого уровня.)
Следующий вызов возвращает точно такую же табличку, что и выше:
unround(x = 3,5, цифры = 2, округление = "вверх") #> # Таблица: 1 × 7 #> округление диапазона ниже incl_lower x incl_upper выше #>#> 1 3,495 <= x(3,5) < 3,505 up 3,50 ИСТИНА 3,5 ЛОЖЬ 3,50
Поскольку x векторизованы, вы можете протестировать несколько
числа сразу:
vec2 <- c(2, 3.1, 3.5) %>% восстановить_нули() vec2 # `restore_zeros()` возвращает "2.0" для 2 #> [1] "2.0" "3.1" "3.5" vec2 %>% не округлять (округление = "четное") #> # Буквы: 3 × 7 #> округление диапазона ниже incl_lower x incl_upper выше #>
#> 1 1.95 < x(2,0) < 2,05 даже 1,95 ЛОЖЬ 2,0 ЛОЖЬ 2,05 #> 2 3.05 < x(3.1) < 3.15 даже 3.05 ЛОЖЬ 3.1 ЛОЖЬ 3.15 #> 3 3,45 < x(3,5) < 3,55 четный 3,45 ЛОЖЬ 3,5 ЛОЖЬ 3,55
Дробное округление
Что делать, если вы хотите округлить числа до дроби, а не до
целое число? Проверьте reround_to_fraction() и
reround_to_fraction_level() :
reround_to_fraction (x = 0,4, знаменатель = 2, округление = «вверх») #> [1] 0,5
Эта функция округляет 0,4 до 0,5 , потому что
это ближайшая дробь 2 . Это вдохновлено
janitor::round_to_fraction() и кредит на ядро
реализация идет туда. reround_to_fraction() смесей
дробное округление уборщика с гибкостью и точностью,
reround() обеспечивает.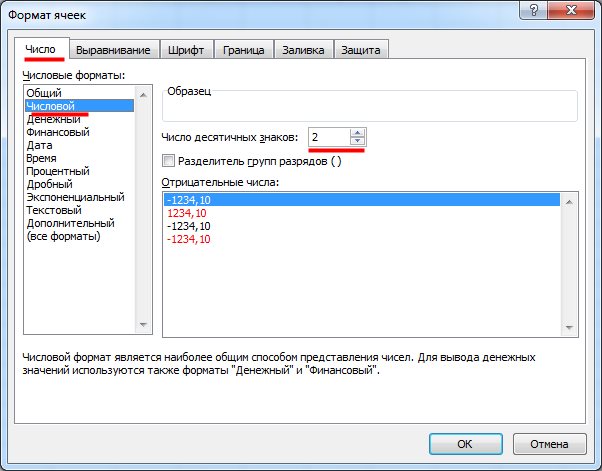
Более того, reround_to_fraction_level() округляет до
ближайшая дробь на десятичном уровне, указанном через его
цифр аргумент:
reround_to_fraction_level( x = 0,777, знаменатель = 5, цифры = 0, округление = «в меньшую сторону» ) #> [1] 0,8 reround_to_fraction_level( x = 0,777, знаменатель = 5, цифры = 1, округление = «в меньшую сторону» ) #> [1] 0,78 reround_to_fraction_level( x = 0,777, знаменатель = 5, цифры = 2, округление = «в меньшую сторону». ) #> [1] 0.776
Эти две функции в настоящее время не являются частью какого-либо обнаружения ошибок
рабочий процесс.
Смещение округления
Выше я писал, что округление в большую или меньшую сторону от 5 является смещенным. Однако,
это указывает на более широкую проблему: это верно для любой процедуры округления
который не принимает активных мер предосторожности против такого предубеждения.
base::round() делает, и поэтому я рекомендую его для
оригинальная работа (в отличие от реконструкции).
Возможно, было бы полезно иметь общий и гибкий способ количественной оценки того, как
сильное округление искажает распределение по сравнению с тем, как оно выглядело
до округления. Функция rounding_bias() выполняет это
роль. Это оболочка вокруг reround() , поэтому он может получить доступ
любая процедура округления, которую может выполнить reround() , и принимает все
те же аргументы. Однако по умолчанию для округление равно
"вверх" вместо "вверх_или_вниз" , потому что
rounding_bias() имеет смысл только с однократным округлением
процедуры.
Обычно смещение из-за округления вычисляется путем вычитания
исходная раздача из округленной:
\[
смещение = x_{округлено} - x
\]
По умолчанию вычисляется среднее значение, чтобы уменьшить погрешность до единичных данных
точка:
vec3 <- seq(от = 0,6, до = 0,7, по = 0,01) vec3 #> [1] 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,690,70 # Среднее значение до округления... среднее (vec3) #> [1] 0,65 # ...не то, что потом... среднее (округление (vec3)) #> [1] 1 # ...и разница в смещении: rounding_bias (x = vec3, цифры = 0, округление = «вверх») #> [1] 0.35
Установить означает на FALSE , чтобы вернуть целое
вместо этого вектор отдельных смещений:
rounding_bias (x = vec3, digits = 0, округление = «вверх», среднее = FALSE) #> [1] 0,40 0,39 0,38 0,37 0,36 0,35 0,34 0,33 0,32 0,31 0,30
Следует признать, что этот пример несколько преувеличен. Вот довольно
безобидный:
vec4 <- rnorm(50000, 100, 15) rounding_bias (vec4, цифры = 2) #> [1] -7.297672e-06
Что отвечает за такую разницу? Кажется, это (1)
размер выборки и (2) количество знаков после запятой, до которых вектор
округлый. Метод округления не имеет значения, если числа с
многие десятичные знаки округлены:
#> # tibble: 10 × 3
#> смещение округления десятичных_цифр
#>
#> 1 0.00000810 1 вверх вверх
#> 2 0.


 При этом числа с дробной частью от 0,5 до 0,999 округляются до следующего целого числа, а числа от 0 до 0,499 округляются до предыдущего целого числа.
При этом числа с дробной частью от 0,5 до 0,999 округляются до следующего целого числа, а числа от 0 до 0,499 округляются до предыдущего целого числа. д.). В этом случае последние разряды отбрасываются, а предыдущий разряд увеличивается на 1, если отброшенная цифра больше или равна 5.
д.). В этом случае последние разряды отбрасываются, а предыдущий разряд увеличивается на 1, если отброшенная цифра больше или равна 5. Например, число 3,9 округляется до 3.
Например, число 3,9 округляется до 3. n
n 2;
идентификационное имя;
расходы на вар клинику;
БЕГАТЬ;
2;
идентификационное имя;
расходы на вар клинику;
БЕГАТЬ;  2
round_up_from (x = 4,28, цифры = 1, порог = 1)
#> [1] 4.3
2
round_up_from (x = 4,28, цифры = 1, порог = 1)
#> [1] 4.3  ..
#> [1] 4 6 6 8 8 10 10
среднее (vec2)
#> [1] 7.5
среднее (up2)
#> [1] 8
среднее (вниз2)
#> [1] 7
mean(even2) # ... и среднее немного смещено вниз!
#> [1] 7.428571
vec3 <- с(
1,05, 1,15, 1,25, 1,35, 1,45,
1,55, 1,65, 1,75, 1,85, 1,95
)
# Однако здесь нет предвзятости:
раунд (vec3, 1)
#> [1] 1,0 1,1 1,2 1,4 1,4 1,6 1,6 1,8 1,9 2,0
среднее (vec3)
#> [1] 1,5
среднее (раунд (vec3, 1))
#> [1] 1.5
..
#> [1] 4 6 6 8 8 10 10
среднее (vec2)
#> [1] 7.5
среднее (up2)
#> [1] 8
среднее (вниз2)
#> [1] 7
mean(even2) # ... и среднее немного смещено вниз!
#> [1] 7.428571
vec3 <- с(
1,05, 1,15, 1,25, 1,35, 1,45,
1,55, 1,65, 1,75, 1,85, 1,95
)
# Однако здесь нет предвзятости:
раунд (vec3, 1)
#> [1] 1,0 1,1 1,2 1,4 1,4 1,6 1,6 1,8 1,9 2,0
среднее (vec3)
#> [1] 1,5
среднее (раунд (vec3, 1))
#> [1] 1.5  95 <= x(8.0) <= 8.05 up_or_down 7.95 TRUE 8.0 TRUE 8.05
95 <= x(8.0) <= 8.05 up_or_down 7.95 TRUE 8.0 TRUE 8.05  50) < 3.505 up 3.50 TRUE 3.50 FALSE 3.50
50) < 3.505 up 3.50 TRUE 3.50 FALSE 3.50  1, 3.5) %>%
восстановить_нули()
vec2 # `restore_zeros()` возвращает "2.0" для 2
#> [1] "2.0" "3.1" "3.5"
vec2 %>%
не округлять (округление = "четное")
#> # Буквы: 3 × 7
#> округление диапазона ниже incl_lower x incl_upper выше
#>
1, 3.5) %>%
восстановить_нули()
vec2 # `restore_zeros()` возвращает "2.0" для 2
#> [1] "2.0" "3.1" "3.5"
vec2 %>%
не округлять (округление = "четное")
#> # Буквы: 3 × 7
#> округление диапазона ниже incl_lower x incl_upper выше
#>  ..
среднее (vec3)
#> [1] 0,65
# ...не то, что потом...
среднее (округление (vec3))
#> [1] 1
# ...и разница в смещении:
rounding_bias (x = vec3, цифры = 0, округление = «вверх»)
#> [1] 0.35
..
среднее (vec3)
#> [1] 0,65
# ...не то, что потом...
среднее (округление (vec3))
#> [1] 1
# ...и разница в смещении:
rounding_bias (x = vec3, цифры = 0, округление = «вверх»)
#> [1] 0.35