Содержание
округление и другие действия с числами
Навигация по уроку
- Функция SQL ROUND
- Функция SQL CEILING
- Функция SQL FLOOR
- Другие функции SQL для работы с числами
Связанные темы
- Оператор SELECT
- Агрегатные функции
| Назад | Содержание | Вперёд>>> |
Функция SQL ROUND(результат_вычислений, n) округляет результат вычислений до n-го знака после запятой.
Округление производится по правилам арифметики.
Если n — отрицательное число (−n), то округление происходит до n-го знака перед запятой. Таким образом,
с помощью функции ROUND можно получить и целое число как результат округления.
Пример 1. В базе данных фирмы есть таблица Staff, содержащая
данные о сотрудниках фирмы. Выведем индивидуальные размеры заработной платы сотрудников:
Выведем индивидуальные размеры заработной платы сотрудников:
SELECT Name, Salary
FROM STAFF
Результатом выполнения запроса будет следующая таблица:
| Name | Salary |
| Sanders | 18357.5 |
| Pernal | 15430.0 |
| Marenghi | 17506.8 |
| Doctor | 12322.8 |
| Factor | 16228.7 |
| Junkers | 16232.8 |
| Moonlight | 21500.6 |
| Aisen | 19540.7 |
| MacGregor | 15790.8 |
Для вычисления среднего размера заработной платы пишем запрос:
SELECT AVG(Salary)
FROM STAFF
Получим следующий результат:
| AVG(Salary) |
| 16990.06662326389 |
Для отчётов результат с таким числом знаков после запятой не годится. Округлим результат до второго
знака после запятой с помощью функции ROUND:
SELECT ROUND(AVG(Salary),2)
AS Avg_Salary
FROM STAFF
Результат будет следующим:
| Avg_Salary |
16990. 07 07 |
- Страница 2. Другие функции SQL для работы с числами
Пример 2. Теперь округлим результат до первого знака до запятой,
применяя в функции ROUND параметр минус единица:
SELECT ROUND(AVG(Salary),−1)
AS Avg_Salary
FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 16990 |
Сместим округление ещё на один знак влево и применим в функции ROUND параметр минус 2:
SELECT ROUND(AVG(Salary),−2)
AS Avg_Salary
FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 17000 |
Функция SQL ROUND может применяться ещё и с третьим необязательными параметром
(кроме MySQL). Если этим параметром будет 1, то округление производиться не будет, просто в результате
будет оставлено столько знаков после запятой, сколько указано во втором параметре.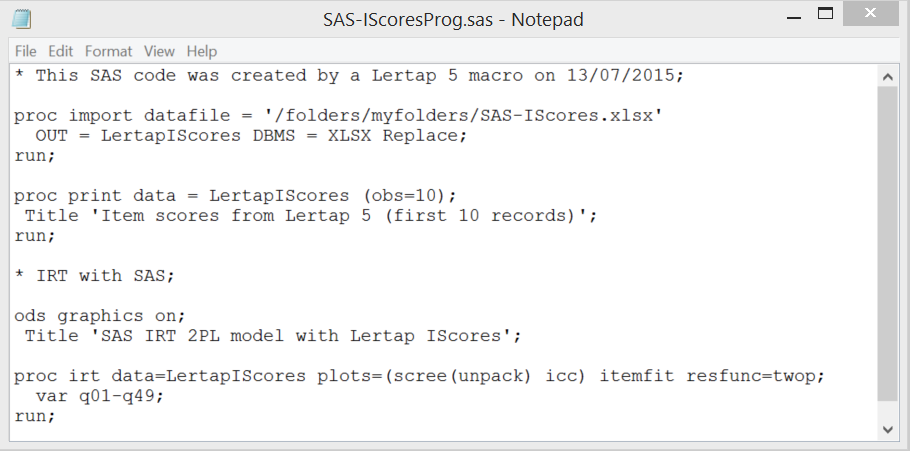
Пример 3. Оставить в результате вычислений средней заработной
платы два знака после запятой, не производя округления. Применяем функцию ROUND с тремя параметрами:
SELECT ROUND(AVG(Salary),2,1)
AS Avg_Salary
FROM STAFF
Результат будет следующим:
| Avg_Salary |
| 16990.06 |
- Страница 2. Другие функции SQL для работы с числами
Функция MySQL TRUNCATE
В MySQL аналогом разновидности функции ROUND без округления результата является функция TRUNCATE.
Она, как и ROUND в общем случае имеет два параметра: результат вычислений и число знаков после запятой.
Пример 4. Условие то же, что в примере 3, но в MySQL. Применяем
функцию TRUNCATE:
SELECT TRUNCATE(AVG(Salary),2)
AS Avg_Salary
FROM STAFF
Получим результат без округления, как в предыдущем примере:
| Avg_Salary |
16990.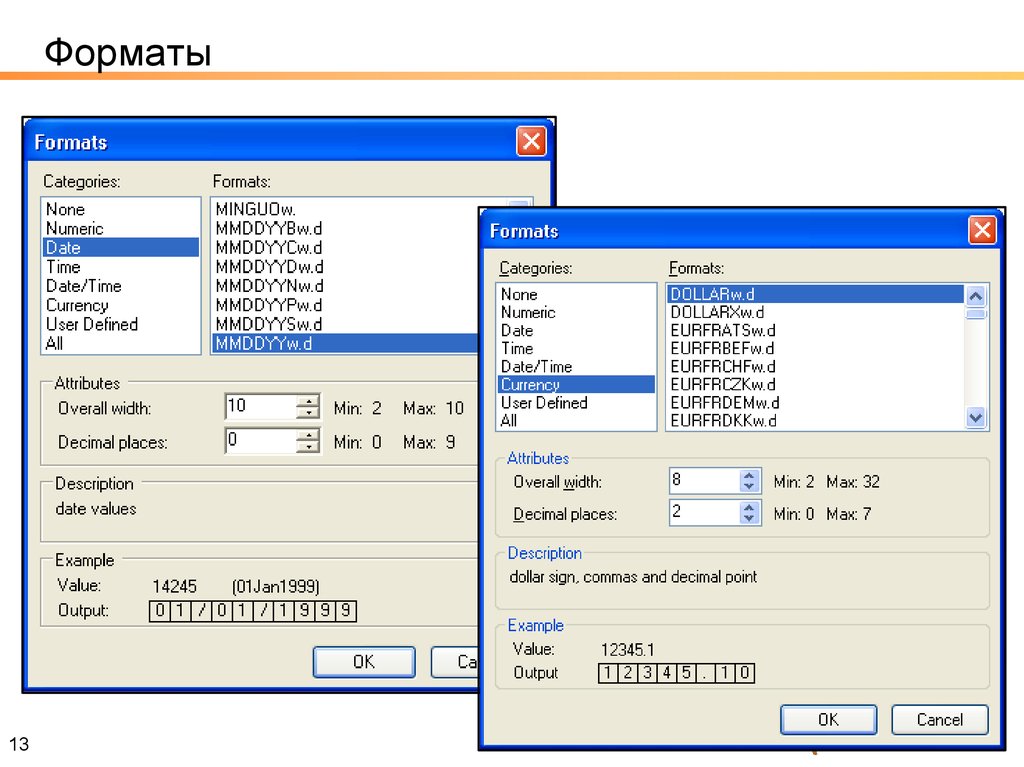 06 06 |
- Страница 2. Другие функции SQL для работы с числами
Функция SQL CEILING не производит округления. Она просто принимает дробное число и возвращает максимальное
целое число, не меньшее принятого. Приведём примеры действия функции с различными принятыми дробными числами.
| Функция с аргументом | Возвращаемое значение |
| CEILING(0.38) | 1 |
| CEILING(1.63) | 2 |
| CEILING(−0.38) | 0 |
| CEILING(−1.63) | −1 |
В случае функции CEILING некорректно говорить об округлении, поскольку она преобразует числа без
учёта правил арифметики.
- Страница 2. Другие функции SQL для работы с числами
Функция FLOOR также не производит округления. Её действие противоположно действию функции CEILING.
Она принимает дробное число и возвращает максимальное
целое число, не большее принятого.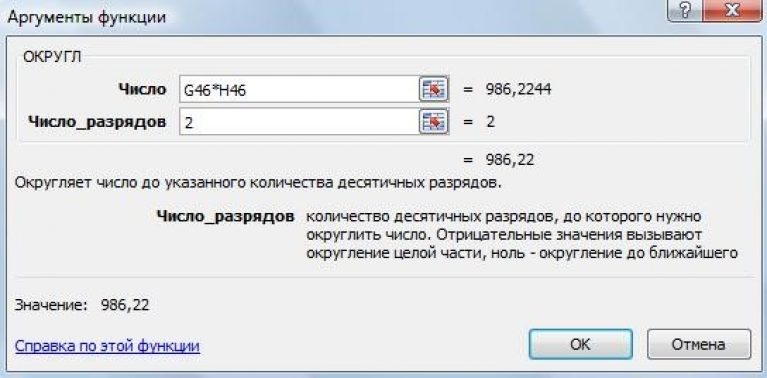 Приведём примеры действия функции с различными принятыми дробными числами.
Приведём примеры действия функции с различными принятыми дробными числами.
| Функция с аргументом | Возвращаемое значение |
| FLOOR(0.38) | 0 |
| FLOOR(1.63) | 1 |
| FLOOR(−0.38) | −1 |
| FLOOR(−1.63) | −2 |
Функция FLOOR, как и функция CEILING, преобразует числа без
учёта правил арифметики.
- Страница 2. Другие функции SQL для работы с числами
Поделиться с друзьями
| Назад | Содержание | Вперёд>>> |
SAS — Числовые форматы — CoderLessons.com
SAS может обрабатывать различные форматы числовых данных. Эти форматы используются в конце имен переменных для применения определенного числового формата к данным. SAS использует два вида числовых форматов. Один для чтения определенных форматов числовых данных, который называется informat, и другой для отображения числовых данных в определенном формате, называемом выходным форматом .
Синтаксис
Синтаксис для числовой информации –
Varname Formatnamew.d
Ниже приведено описание используемых параметров:
Varname – это имя переменной.
Formatname – это имя имени числового формата, примененного к переменной.
w – максимальное количество столбцов данных (включая цифры после десятичной точки и саму десятичную точку), разрешенных для хранения для переменной.
d – количество цифр справа от десятичной дроби.
Varname – это имя переменной.
Formatname – это имя имени числового формата, примененного к переменной.
w – максимальное количество столбцов данных (включая цифры после десятичной точки и саму десятичную точку), разрешенных для хранения для переменной.
d – количество цифр справа от десятичной дроби.
Чтение Числовых форматов
Ниже приведен список форматов, используемых для чтения данных в SAS.
Числовые форматы ввода
| Формат | использование |
|---|---|
| п. | Максимальное количество столбцов “n” без десятичной точки. |
| н.п. | Максимальное количество столбцов с n-кратными точками “n”. |
| COMMAn.p | Максимальное число столбцов «n» с десятичными знаками «p», которое удаляет любые запятые или знаки доллара. |
| COMMAn.p | Максимальное число столбцов «n» с десятичными знаками «p», которое удаляет любые запятые или знаки доллара |
Максимальное количество столбцов “n” без десятичной точки.
Максимальное количество столбцов с n-кратными точками “n”.
Максимальное число столбцов «n» с десятичными знаками «p», которое удаляет любые запятые или знаки доллара.
Максимальное число столбцов «n» с десятичными знаками «p», которое удаляет любые запятые или знаки доллара
Отображение числовых форматов
Аналогично применению формата при чтении данных, ниже приведен список форматов, используемых для отображения данных в выходных данных программы SAS.
Числовые форматы вывода
| Формат | использование |
|---|---|
| п. | Запишите максимальное количество цифр «n» без десятичной точки. |
| н.п. | Запишите максимальное число столбцов «np» с десятичными точками «p». |
| DOLLARn.p | Запишите максимальное число столбцов с «n» с p десятичными знаками, начальным знаком доллара и запятой на тысячном месте. |
Запишите максимальное количество цифр «n» без десятичной точки.
Запишите максимальное число столбцов «np» с десятичными точками «p».
Запишите максимальное число столбцов с «n» с p десятичными знаками, начальным знаком доллара и запятой на тысячном месте.
Пожалуйста, обратите внимание –
Если количество цифр после десятичной точки меньше спецификатора формата, то в конце будут добавлены нули .
Если количество цифр после десятичной точки больше, чем спецификатор формата, то последняя цифра округляется .

Если количество цифр после десятичной точки меньше спецификатора формата, то в конце будут добавлены нули .
Если количество цифр после десятичной точки больше, чем спецификатор формата, то последняя цифра округляется .
Примеры
Ниже приведены примеры, иллюстрирующие приведенные выше сценарии.
DATA MYDATA1; input x 6.; /*maxiiuum width of the data*/ format x 6.3; datalines; 8722 93.2 .1122 15.116 PROC PRINT DATA = MYDATA1; RUN; DATA MYDATA2; input x 6.; /*maximum width of the data*/ format x 5.2; datalines; 8722 93.2 .1122 15.116 PROC PRINT DATA = MYDATA2; RUN; DATA MYDATA3; input x 6.; /*maximum width of the data*/ format x DOLLAR10.2; datalines; 8722 93.2 .1122 15.116 PROC PRINT DATA = MYDATA3; RUN;
Когда мы выполняем приведенный выше код, он дает следующий результат –
6.8 — Форматирование значений данных
Следующая программа SAS иллюстрирует использование оператора FORMAT для указания SAS отображать переменную расход с использованием формата доллара9. 2 :
2 :
PROC PRINT data = basic LABEL;
имя метки = 'Имя'
клиника = 'Клиника'
расход = 'Расход';
формат счет доллара9.2;
идентификационное имя;
расходы на вар клинику;
БЕЖАТЬ; | Имя | Поликлиника | Расход |
|---|---|---|
| Элис Смит | ЛЬЮН | 1001,98 $ |
| Мэриэнн Уайт | ЛЬЮН | 2 999,34 $ |
| Томас Джонс | АЛЬТО | 3904,89 $ |
| Бенедиктин Арнольд | АЛЬТО | 1450,23 $ |
| Фелиция Хо | МНМК | 1 209,94 $ |
| Джон Смит | МНМК | 1 763,09 $ |
| Джейн Смайли | МНМК | 3 567,00 $ |
Оператор FORMAT сообщает SAS, что на время выполнения процедуры PRINT формат 9,2 долларов должен быть связан с переменной расход . Как только процедура PRINT закрывается, ассоциация больше не сохраняется. Формат доллара 9,2 указывает SAS отображать расходы 9.0004 значения с использованием знаков доллара, запятых (при необходимости) и двух знаков после запятой. 9 сообщает SAS, что для размещения каждого значения расходов потребуется не более 9 пробелов — 1 для знака доллара, 1 для знака запятой, 4 для цифр до запятой, 1 для десятичного знака и 2 для десятичного знака. разместить цифры.
Как только процедура PRINT закрывается, ассоциация больше не сохраняется. Формат доллара 9,2 указывает SAS отображать расходы 9.0004 значения с использованием знаков доллара, запятых (при необходимости) и двух знаков после запятой. 9 сообщает SAS, что для размещения каждого значения расходов потребуется не более 9 пробелов — 1 для знака доллара, 1 для знака запятой, 4 для цифр до запятой, 1 для десятичного знака и 2 для десятичного знака. разместить цифры.
Запустите и запустите программу SAS и просмотрите полученный результат, чтобы убедиться, что значения переменных расхода были напечатаны, как описано. Затем вы можете изменить 9в формате доллара9,2 на 8 и повторно запустите программу SAS, чтобы убедиться, что SAS опускает запятую, чтобы значения помещались в восемь выделенных пробелов. Затем, если вам все еще нравится, вы можете изменить весь формат доллара9,2 на формат запятая8,2 и повторно запустить программу SAS, чтобы ознакомиться с форматом запятой.
Как правило, для каждой переменной можно использовать отдельный оператор FORMAT или можно форматировать несколько переменных в одном операторе FORMAT. В таблице ниже показаны некоторые из наиболее часто используемых форматов SAS:
| Формат | Указывает эти значения | Пример |
| ЗАПЯТАЯ w . д | , содержащие запятые и десятичные разряды | запятая8.2 |
| ДОЛЛАР б.д. | , содержащие знаки доллара, запятые и десятичные разряды | доллар 6,2 |
| ММДДГГ w . | как значения даты в форме 03.10.08 ( ммддгг8 .) или 03.10.2008 ( ммддгг10 .) | ммдддгг10. |
| ш . | округляется до ближайшего целого числа в w пробелах | 7. |
ш. д д | округляется до d десятичных знаков в w пробелах | 8,2 |
| $ в . | как символьные значения в пробелах w | 12 долларов. |
| ДАТА w . | как значения даты формы 02OCT08 ( date7.) или 02OCT2008 ( date9.) | дата9. |
Конечно, другие доступные форматы можно найти в справке и документации SAS.
Имельда С. Го, Департамент образования Южной Каролины … Flipbook PDF
Материалы SESUG (c) SESUG, Inc (http://www.sesug.org) Документы, содержащиеся в материалах SESUG, являются собственностью их авторов, если не указано иное. Не перепечатывать без разрешения. Документы SESUG распространяются бесплатно благодаря любезности Института продвинутой аналитики (http://analytics.ncsu.edu). PO–082
Округление в SAS®: предотвращение проблем с числовым представлением Имельда С. Го, Департамент образования Южной Каролины, Колумбия, Южная Каролина РЕЗЮМЕ Как программисты SAS мы имеем разный опыт. Мы варьируемся от небольшого или нулевого формального образования в области компьютерных наук до академических степеней в области компьютерных наук. Числовая точность и представление являются стандартными темами в обучении информатике. Со временем программисты сталкиваются с проблемами точности и представления чисел. Связанные с ними проблемы особенно опасны, когда программист не знает об их наличии и, следовательно, не предпринимает действий по программированию для решения таких проблем. Например, мы можем заметить, что наши числовые результаты сравнения не соответствуют нашим ожиданиям. Рассмотрим утверждение SAS: «Если 0,3=3*0,1, то равно = ‘Y’; иначе равно=’N’;” Если вы считаете, что результат Y, то эту статью необходимо прочитать. К счастью, есть шаги, которые вы можете предпринять, чтобы предотвратить подобные проблемы.
Го, Департамент образования Южной Каролины, Колумбия, Южная Каролина РЕЗЮМЕ Как программисты SAS мы имеем разный опыт. Мы варьируемся от небольшого или нулевого формального образования в области компьютерных наук до академических степеней в области компьютерных наук. Числовая точность и представление являются стандартными темами в обучении информатике. Со временем программисты сталкиваются с проблемами точности и представления чисел. Связанные с ними проблемы особенно опасны, когда программист не знает об их наличии и, следовательно, не предпринимает действий по программированию для решения таких проблем. Например, мы можем заметить, что наши числовые результаты сравнения не соответствуют нашим ожиданиям. Рассмотрим утверждение SAS: «Если 0,3=3*0,1, то равно = ‘Y’; иначе равно=’N’;” Если вы считаете, что результат Y, то эту статью необходимо прочитать. К счастью, есть шаги, которые вы можете предпринять, чтобы предотвратить подобные проблемы.
Примечание. Из-за различий в аппаратных ограничениях и операционных системах приведенные ниже примеры SAS для ПК могут отличаться от результатов на других компьютерных системах. Общепринятого метода выполнения вычислений в компьютерных системах не существует.
Общепринятого метода выполнения вычислений в компьютерных системах не существует.
НЕ ВСЕ ЧИСЛА МОГУТ ТОЧНО ПРЕДСТАВИТЬ НА КОМПЬЮТЕРЕ Точность чисел (то есть точность, с которой число может быть представлено) и представление в компьютерах являются корнем проблемы. SAS использует представление с плавающей запятой (т. е. реальное двоичное). Исходное десятичное число и число, представленное в двоичном виде, могут быть очень близки, но очень близко не равнозначно равенству. Точного двоичного представления для десятичных значений 0,1 и 0,3 не существует, что объясняет разницу в примере № 1 ниже. Преимуществом представления с плавающей запятой является скорость, а недостатком — ошибка представления. Повторяющиеся десятичные и иррациональные числа — другие очевидные проблемы для точного хранения на компьютере. Например, 1/3 равна десятичной точке, за которой следует бесконечное количество троек. Компьютеры не могут хранить бесконечное количество цифр. Нам нужно различать ожидаемый математический результат (наши десятичные значения) и то, что компьютер может хранить (двоичные значения) и соответствующим образом программировать. Читатели могут обратиться к двум справочным материалам по технической поддержке SAS (TS-230 и TS654), перечисленным в конце этого документа, за подробными пояснениями и примерами, касающимися представления с плавающей запятой.
Читатели могут обратиться к двум справочным материалам по технической поддержке SAS (TS-230 и TS654), перечисленным в конце этого документа, за подробными пояснениями и примерами, касающимися представления с плавающей запятой.
ПРИМЕР №1 Мы знаем математический факт, что 3 умножить на 0,1 равно 0,3. Поэтому, когда мы исследуем следующий код ниже, кажется разумным ожидать, что равная переменная будет иметь значение Y, потому что обе переменные разрешаются в 0,3 (по крайней мере, математически).
Если вы думаете, что единственный возможный ответ — Y, то вас ждет сюрприз! Давайте посмотрим на вывод PROC PRINT для набора данных выше.
Если мы используем следующий оператор с PROC PRINT, формат значение1 значение2 32.31;
1
получаем следующий вывод.
Оба значения равны 0,3, но это только то, что касается вывода PROC PRINT. Эти два значения хранятся в компьютере по-разному. На следующей странице мы отмечаем, что форматы SAS округляются, и поэтому мы не можем увидеть разницу в значениях. Чтобы увидеть, как различаются значения, воспользуемся HEX16. формат с помощью PROC PRINT. формат значение1 значение2 шестнадцатеричный16.; Мы получаем следующий вывод, который показывает разницу между двумя значениями.
Чтобы увидеть, как различаются значения, воспользуемся HEX16. формат с помощью PROC PRINT. формат значение1 значение2 шестнадцатеричный16.; Мы получаем следующий вывод, который показывает разницу между двумя значениями.
ПРИМЕР #2 Вот еще один пример. Разница между обеими парами чисел математически равна 3,8, но сравнение не удается.
Без указания формата получаем следующие результаты.
Если мы используем следующий оператор с PROC PRINT, разница в формате 32.31; мы получаем следующий вывод.
2
ПРИМЕР #3 Ошибка репрезентации может стать серьезной проблемой, если человек даже не подозревает, что она может произойти, и не принимает никаких мер против нее. Неучтенный размер ошибок или несоответствий может накапливаться в течение нескольких операций. Давайте возьмем простой пример добавления 0,1 десять триллионов раз. Мы знаем, что результат должен быть один триллион.
После сложения всех этих чисел SAS выдает следующее.
За очень много вычислений разница накопилась до 163. 124. Насколько это серьезно? Все зависит от ваших данных. Для кого-то это может быть терпимо, а для кого-то совершенно неприемлемо. Еще следует подумать о том, что происходит с другими результатами, когда испорченная сумма используется в других вычислениях.
124. Насколько это серьезно? Все зависит от ваших данных. Для кого-то это может быть терпимо, а для кого-то совершенно неприемлемо. Еще следует подумать о том, что происходит с другими результатами, когда испорченная сумма используется в других вычислениях.
РЕШЕНИЕ ПРОБЛЕМЫ Мы несем ответственность за наши данные, программы и результаты. Первым шагом в решении проблемы является определение проблемы и осознание условий, при которых проблема может привести к нежелательным результатам. Что касается области компьютерных наук, это известная проблема. «Большинство опубликованных алгоритмов численного анализа предназначены для учета и сведения к минимуму влияния ошибки представления». (TS-230) «К сожалению, не существует единого метода, который лучше всего справляется с проблемами, вызванными ошибкой числового представления. То, что является идеальным решением для одного приложения, может резко повлиять на производительность и результаты другого приложения». (TS-230) Таким образом, эта статья посвящена простейшим примерам этой проблемы.
Стратегия выживания № 1: Сохранить целое Самый безопасный способ — просто иметь дело с целыми числами или целыми числами. Если на компьютере результаты операций над целыми числами всегда являются целыми числами, тогда нет проблем, поскольку целое число может храниться точно в компьютерах, пока не превышено максимальное целочисленное значение, которое может представить компьютер. Сможете ли вы остаться в области целых чисел, зависит от того, какие данные задействованы и что нужно сделать с данными. Если вы не просто складываете, вычитаете и умножаете целые числа на целые числа, вы можете столкнуться с нецелым числом, когда придет время делить целое число на другое целое число. Рассмотрим следующий пример, который может представлять собой денежные суммы, такие как доллары и центы.
Введенные значения были умножены на масштабный коэффициент 100 (чтобы «перевести» цифры после двух знаков после запятой в целую часть числа). Функция INT, которая возвращает целочисленное значение аргумента, затем применяется для устранения ошибки представления, которая могла быть вызвана десятичной или дробной частью входных данных.
3
Вы можете приступить к применению целочисленной арифметики к целочисленным значениям. Когда вы достигнете последнего целочисленного арифметического результата, вы можете разделить его на 100, чтобы восстановить десятичную часть. Вы также можете применить аналогичную стратегию к процентам. Проценты, например 18%, можно умножить на 100 и сохранить как 18.
Стратегия преодоления № 2: Не бойтесь сравнивать с округленными числами В приведенных выше примерах № 1– № 3 ошибка представления проявлялась при сравнении значений. TS-654 рекомендует помнить следующее при работе с нецелыми или действительными числами в целом: 9 9 9 9
Знайте свои данные. Определитесь с уровнем значимости, который вам нужен. Помните, что все числовые значения хранятся в представлении с плавающей запятой. Используйте функции сравнения, такие как ОКРУГЛ.
Вы можете применить функцию ОКРУГЛ в стратегических точках процесса вычислений (например, в конце серии вычислений, после каждого вычисления). То, что вы делаете, зависит от характера данных, того, что вы должны делать с данными, и когда ошибка представления может стать проблемой. Прежде чем выполнять сравнение на равенство, вы можете округлить один или оба операнда. Альтернативой округлению является указание, в какой степени два значения достаточно близки, чтобы их можно было считать хорошими и равными с точки зрения вашего программирования SAS. Этот процесс называется фаззингом сравнения. См. примеры в TS-230. Функция ОКРУГЛ имеет следующий синтаксис: ОКРУГЛ (аргумент) Она округляет первый аргумент до ближайшего кратного второго аргумента. Если единица округления не указана, она округляется до ближайшего целого числа. ® САС 9Справочный словарь языка заверяет нас, что мы можем ожидать получения десятичных арифметических результатов, если результат содержит не более девяти значащих цифр и выполняется любое из следующих условий: 9 Единицей округления является целое число или степень 10, большая или равная к 1Е-15. 9 Ожидаемый десятичный арифметический результат имеет не более четырех знаков после запятой.
То, что вы делаете, зависит от характера данных, того, что вы должны делать с данными, и когда ошибка представления может стать проблемой. Прежде чем выполнять сравнение на равенство, вы можете округлить один или оба операнда. Альтернативой округлению является указание, в какой степени два значения достаточно близки, чтобы их можно было считать хорошими и равными с точки зрения вашего программирования SAS. Этот процесс называется фаззингом сравнения. См. примеры в TS-230. Функция ОКРУГЛ имеет следующий синтаксис: ОКРУГЛ (аргумент) Она округляет первый аргумент до ближайшего кратного второго аргумента. Если единица округления не указана, она округляется до ближайшего целого числа. ® САС 9Справочный словарь языка заверяет нас, что мы можем ожидать получения десятичных арифметических результатов, если результат содержит не более девяти значащих цифр и выполняется любое из следующих условий: 9 Единицей округления является целое число или степень 10, большая или равная к 1Е-15. 9 Ожидаемый десятичный арифметический результат имеет не более четырех знаков после запятой. ® Обратитесь к Справочному словарю языка SAS 9 для получения более подробной информации о функции ОКРУГЛ. Если функция ОКРУГЛ не соответствует вашим потребностям, вы можете указать свой собственный коэффициент нечеткости для использования с функцией ОКРУГЛ. В TS-230 приведены примеры того, как это сделать.
® Обратитесь к Справочному словарю языка SAS 9 для получения более подробной информации о функции ОКРУГЛ. Если функция ОКРУГЛ не соответствует вашим потребностям, вы можете указать свой собственный коэффициент нечеткости для использования с функцией ОКРУГЛ. В TS-230 приведены примеры того, как это сделать.
Давайте изменим ПРИМЕР #1, включив функцию ОКРУГЛ для обоих значений.
На этот раз можно ожидать правильных математических результатов, поскольку функция ОКРУГЛ возвращает значение, основанное на десятичной арифметике, путем округления значений до первого десятичного знака.
4
Давайте изменим ПРИМЕР #2, включив в него функцию ОКРУГЛ в точке сравнения.
Давайте изменим ПРИМЕР #3, чтобы включить функцию ОКРУГЛ каждый раз, когда происходит сложение.
Несколько слов о форматах SAS Предположим, у вас есть числа, которые были сохранены с ошибкой числового представления, и все, что вы хотите сделать, это распечатать их с математически правильными значениями. Согласно ТС-230 числовые форматы круглые. HEX16. формат является исключением (т. е. он отображает точное значение переменной в точном шестнадцатеричном представлении 8-байтового числа с плавающей запятой). Другим исключением является определяемый пользователем формат PICTURE, который по умолчанию усекается в PROC FORMAT. Форматы влияют на то, как числа отображаются, и не влияют на то, как они хранятся или представляются внутри.
Согласно ТС-230 числовые форматы круглые. HEX16. формат является исключением (т. е. он отображает точное значение переменной в точном шестнадцатеричном представлении 8-байтового числа с плавающей запятой). Другим исключением является определяемый пользователем формат PICTURE, который по умолчанию усекается в PROC FORMAT. Форматы влияют на то, как числа отображаются, и не влияют на то, как они хранятся или представляются внутри.
5
Функции, которые могут оказаться полезными Функции ОКРУГЛ и ЦЕЛОЕ — не единственные средства защиты от проблем с числовым представлением. Какие функции вы используете, зависит от характера ваших данных и вычислений. Вот список функций, описанных в справочнике по языку SAS® 9: словарь, которые могут оказаться полезными или полезными при разработке стратегий для решения подобных проблем. Функции с нулевым фаззингом (т. е. CEILZ, FLOORZ, INTZ, MODZ, ROUNDZ) не пытаются привести свои результаты к значениям, ожидаемым при десятичной арифметике. Следовательно, они могут привести к неожиданным результатам. В других ситуациях вам, возможно, придется создать собственную функцию в соответствии с вашими конкретными потребностями. ФУНКЦИЯ
В других ситуациях вам, возможно, придется создать собственную функцию в соответствии с вашими конкретными потребностями. ФУНКЦИЯ
SYNTAX
CEIL
CEIL (argument)
CEILZ
CEILZ (argument)
FLOOR
FLOOR (argument)
FLOORZ
FLOORZ (argument)
FUZZ
FUZZ (argument)
INT
Int (аргумент)
INTZ
INTZ (аргумент)
MOD
MOD (Аргумент-1, Аргумент-2)
MODZ
MOD (аргумент-1, аргумент-2)
Раунд
ОКРУГЛ (аргумент)
ОКРУГЛ
ОКРУГЛ (аргумент)
ОКРУГЛZ
ОКРУГЛZ (аргумент)
ОПИСАНИЕ Возвращает наименьшее целое число, большее или равное аргументу, с нечетким алгоритмом, чтобы избежать неожиданных результатов с плавающей запятой (если аргумент находится в пределах 1E -12 целого числа, функция возвращает это целое число.) Возвращает наименьшее целое число, которое больше или равно аргументу, используя фаззинг нуля точечные результаты. (Если аргумент находится в пределах 1E-12 от целого числа, функция возвращает это целое число.) Возвращает наибольшее целое число, которое меньше или равно аргументу, используя фаззинг нуля Возвращает ближайшее целое число, если аргумент находится в пределах 1E-12 Возвращает целочисленное значение, подвергнутое фаззингу, чтобы избежать неожиданных результатов с плавающей запятой (если аргумент находится в пределах 1E-12 от целого числа, функция возвращает это целое число.) Возвращает целую часть аргумента, используя фаззинг нуля. Возвращает остаток от деления первый аргумент вторым аргументом, преобразованным во избежание непредвиденных результатов с плавающей запятой Возвращает остаток от деления первого аргумента на второй аргумент, используя фаззинг нуля Округляет первый аргумент до ближайшего кратного второго аргумента или до ближайшее целое, если второй аргумент опущен Округляет первый аргумент до ближайшего кратного второго аргумента и возвращает четное кратное, если первый аргумент находится на полпути между двумя ближайшими m ultiples Округляет первый аргумент до ближайшего кратного второго аргумента с нулевым фаззингом
(Если аргумент находится в пределах 1E-12 от целого числа, функция возвращает это целое число.) Возвращает наибольшее целое число, которое меньше или равно аргументу, используя фаззинг нуля Возвращает ближайшее целое число, если аргумент находится в пределах 1E-12 Возвращает целочисленное значение, подвергнутое фаззингу, чтобы избежать неожиданных результатов с плавающей запятой (если аргумент находится в пределах 1E-12 от целого числа, функция возвращает это целое число.) Возвращает целую часть аргумента, используя фаззинг нуля. Возвращает остаток от деления первый аргумент вторым аргументом, преобразованным во избежание непредвиденных результатов с плавающей запятой Возвращает остаток от деления первого аргумента на второй аргумент, используя фаззинг нуля Округляет первый аргумент до ближайшего кратного второго аргумента или до ближайшее целое, если второй аргумент опущен Округляет первый аргумент до ближайшего кратного второго аргумента и возвращает четное кратное, если первый аргумент находится на полпути между двумя ближайшими m ultiples Округляет первый аргумент до ближайшего кратного второго аргумента с нулевым фаззингом
ССЫЛКИ ® SAS Institute Inc.

