Цилиндрическая форма с дномP45310Верхний диаметр 5,7 см, нижний диаметр 5,3 см, высота 4,6 см, вес по сыру 80 грамм | Цилиндрическая форма с дномP00807Верхний диаметр 8,4 см, нижний диаметр 6 см, высота 6,2 см, вес по сыру 200 грамм | Цилиндрическая форма с дномP00604Верхний диаметр 7,5 см, нижний диаметр 7 см, высота 9 см, вес по сыру 200 грамм |
Цилиндрическая форма с дномP00767Верхний диаметр 6,7 см, нижний диаметр 5,5 см, высота 11 см, вес по сыру 250 грамм | Цилиндрическая форма с дномP00718Верхний диаметр 7,6 см, нижний диаметр 6,8 см, высота 14 см, вес по сыру 300-500 грамм | Цилиндрическая форма с дномP00678Верхний диаметр 9,5 см, нижний диаметр 9,3 см, высота 7 см, вес по сыру 300/400 грамм |
Цилиндрическая форма с дномP00627Верхний диаметр 9,6 см, нижний диаметр 9 см, высота 9,2 см, вес по сыру 300/400 грамм | Цилиндрическая форма с дномP00605Верхний диаметр 18 см, нижний диаметр 17,5 см, высота 9,2 см, вес по сыру 2200 грамм | Цилиндрическая форма с дномP29310Верхний диаметр 12 см, нижний диаметр 11,4 см, высота 13,5 см, вес по сыру 800 грамм |
Цилиндрическая форма с дномP00601Верхний диаметр 14,5 см, нижний диаметр 13,8 см, высота 14 см, вес по сыру 1000 грамм | Цилиндрическая форма с дномP00602Верхний диаметр 15,2 см, нижний диаметр 14,5 см, высота 15 см, вес по сыру 1400 грамм | Цилиндрическая форма с дномP00603Верхний диаметр 16 см, нижний диаметр 15,4 см, высота 15,7 см, вес по сыру 1800 грамм |
Форма для сыраP57310Верхний диаметр 20 см, нижний диаметр 18 см, высота 13 см, вес по сыру 1800 грамм | Форма для сыраP00630Верхний диаметр 18,2 см, нижний диаметр 15 см, высота 18 см, вес по сыру 2000 грамм | Цилиндрическая форма с дномP00662PВерхний диаметр 19,5 см, нижний диаметр 15,5 см, высота 15,5 см, вес по сыру 2000-3000 грамм |
Форма для сыра P57320Верхний диаметр 20 см, нижний диаметр 18 см, высота 14 см, вес по сыру 3000 грамм
| Цилиндрическая форма с дномP00722Диаметр 19 см, высота 18,5 см, вес по сыру 3000 грамм
| Цилиндрическая форма с дномP00606Верхний диаметр 20 см, нижний диаметр 19 см, высота 15,6 см, вес по сыру 3200 грамм |
Цилиндрическая форма с дномP00607Верхний диаметр 22 см, нижний диаметр 21,4 см, высота 16 см, вес по сыру 3500 грамм | Цилиндрическая форма с дномP00754Верхний диаметр 25,5 см, нижний диаметр 25 см, высота 16 см, вес по сыру 4000-5000 грамм | Цилиндрическая форма с дномP00776Верхний диаметр 30,5 см, нижний диаметр 29,5, высота 20 см, вес по сыру 5000-6000 грамм |
Форма для сыра P00802Верхний диаметр 27 см, нижний диаметр 24,5 см, высота 22 см, вес по сыру 5000-6000 грамм | Форма для сыра P57330Верхний диаметр 28 см, нижний диаметр 26 см, высота 16 см, вес по сыру 6000 грамм | Форма для сыра P57340Верхний диаметр 37,5 см, нижний диаметр 26 см, высота 18 см, вес по сыру 15000 грамм |
Цилиндрическая форма для асфальтобетонных образцов ЛО-257 обычн.
 d 101 мм с вкладышами
d 101 мм с вкладышами
Условия доставки и оплаты
С кем мы работаем
Мы готовы к сотрудничеству как с юридическими, так и с физическими лицами
Как происходит оформление заказов
Вы оставляете заявку
Наши менеджеры обрабатывают её
Выставляем счёт или коммерческое предложение
Согласовываем условия оплаты и сроки доставки
Возможные способы оплаты
Наличный расчет
Производится в офисе компании
Безналичный расчет
Физическими лицами осуществляется через онлайн-банк
Юридические лица должны проводить безналичную оплату через расчетный счет. Для этого наши менеджеры подготовят все необходимые документы в электронном виде
Условия получения товаров
Представители юридических лиц должны иметь при себе доверенность на получение Товара и паспорт.
Физическому лицу для получения Товара нужен паспорт.
Адрес выдачи товаров
Выдача товара осуществляется в офисе по адресу:
г.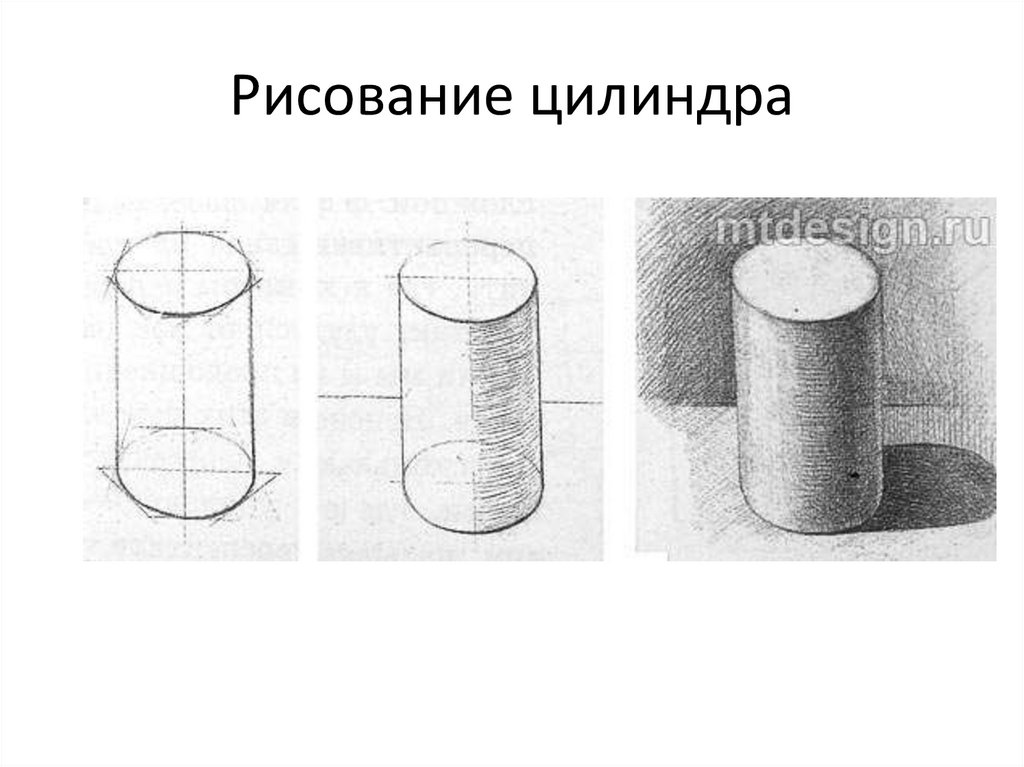 Ростов-на-Дону, ул. Малиновского, 3Д, оф. 723
Ростов-на-Дону, ул. Малиновского, 3Д, оф. 723
Доставка по Ростову-на-Дону
Доставка по городу осуществляется в назначенный день и время.
Стоимость услуги будет зависеть от веса и габаритных размеров Товара
Доставка в другие населенные пункты
Мы готовы отправить Товар в любой населенный пункт России с помощью транспортных компаний:
ООО «Деловые Линии»
ООО «ПЭК»
ООО «Байкал-Сервис»
СДЭК
ООО «Курьер Сервис»
Поставка Товара до терминала в Ростове-на-Дону — бесплатно
Гарантия сохранности
Весь хрупкий Товар для сохранности будет дополнительно упакован в паллетный борт или деревянную обрешетку
Главная » Каталог » Оборудование для лабораторий дорожных и строительных предприятий » Формы для бетона, асфальтобетона
Цена – 10 590 ₽
Рассчет доставки
Выберите курьерскую службу и рассчитайте стоимость доставки товара
Напишите в WhatsApp
Напишите в Viber
Напишите в Telegram
Краткие характеристики
Диаметр формы: 101 мм
- Описание
- Характеристики
- Комплектация
- Документация
Формы ЛО-257 предназначены для определения физико-механических свойств смесей, асфальтобетонов и укрепленных грунтов по ГОСТ 12801.

Форма повышенной прочности ГОСТ 12801-98 за счёт изменения технологии и материалов повышена прочность и твёрдость, увеличен ресурс изделия.
Форма ЛО 257 обычная 101 мм с вкладышами
1. Форма ЛО-257 диам 101 — 1 шт
2. Паспорт — 1 шт
3. Калибровка — 1 шт
Дополнительно:
Комплект пригрузов к ЛО 257 71,4 мм, 101 мм и 50,5 мм
ГОСТ 12801-98
Пригруз к ЛО 257 101 мм
ГОСТ 12801-98
Цилиндр – форма, формула, примеры
Цилиндр – это трехмерная твердая фигура, имеющая два одинаковых круглых основания, соединенных изогнутой поверхностью на определенном расстоянии от центра, которое является высотой цилиндра.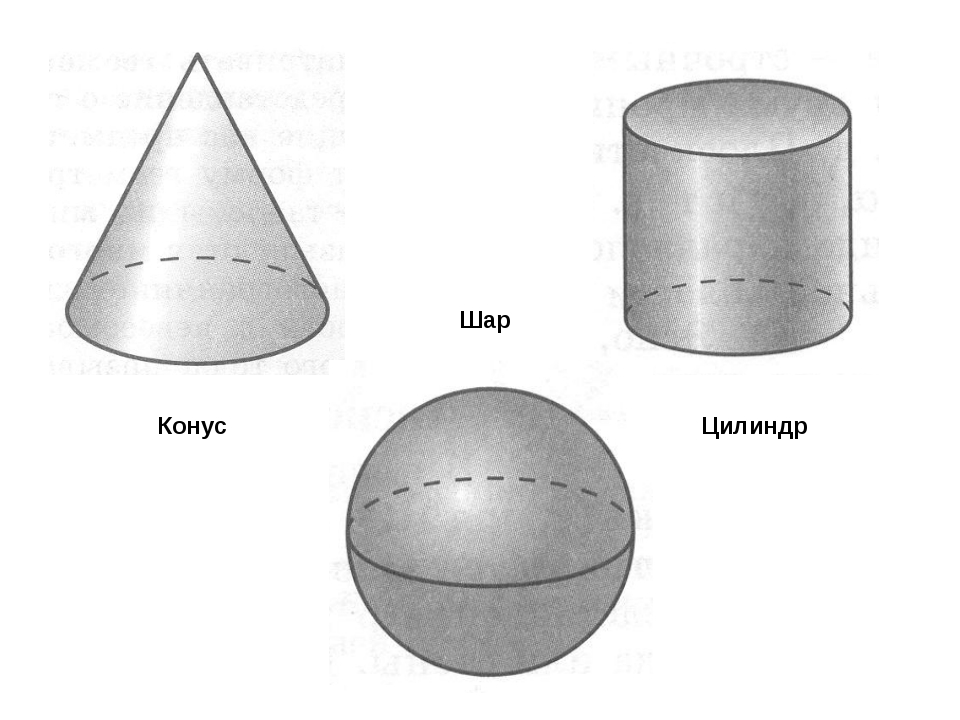 Рулоны туалетной бумаги, банки из-под прохладительных напитков — это реальные примеры цилиндров. А знаете ли вы, что Пизанская башня имеет цилиндрическую форму?
Рулоны туалетной бумаги, банки из-под прохладительных напитков — это реальные примеры цилиндров. А знаете ли вы, что Пизанская башня имеет цилиндрическую форму?
Слово «цилиндр» происходит от греческого слова «kylindros», означающего «валик» или «ролик». Этот термин впервые был использован в математике для описания геометрической формы твердой фигуры с круглым основанием и прямыми сторонами, а позже был применен к другим цилиндрическим объектам, таким как трубы, контейнеры и детали двигателей. Давайте узнаем больше о форме цилиндра в этой статье.
| 1. | Определение цилиндра |
| 2. | Грани цилиндра Вершины Ребра |
| 3. | Типы цилиндров |
| 4. | Свойства цилиндра |
| 5. | Формулы цилиндра |
| 6. | Часто задаваемые вопросы о цилиндре |
Определение цилиндра
Цилиндр представляет собой трехмерное твердое тело, состоящее из двух одинаковых и параллельных оснований, соединенных изогнутой поверхностью. Эти основания подобны круглым дискам. Линия, проходящая из центра или соединяющая центры двух круговых оснований, называется осью формы цилиндра. Расстояние между двумя основаниями называется перпендикулярным расстоянием и обозначается высотой «h». Два круглых основания имеют расстояние от центра до внешней границы, которое известно как радиус цилиндра, обозначенный буквой «r». Цилиндр представляет собой комбинацию 2 кругов + 1 прямоугольник.
Эти основания подобны круглым дискам. Линия, проходящая из центра или соединяющая центры двух круговых оснований, называется осью формы цилиндра. Расстояние между двумя основаниями называется перпендикулярным расстоянием и обозначается высотой «h». Два круглых основания имеют расстояние от центра до внешней границы, которое известно как радиус цилиндра, обозначенный буквой «r». Цилиндр представляет собой комбинацию 2 кругов + 1 прямоугольник.
Посмотрите на данное изображение, показывающее формирование формы цилиндра.
Некоторыми реальными примерами формы цилиндра являются трубы, огнетушители, резервуары для воды, банки из-под прохладительных напитков и т. д.
Грани цилиндра Вершины Ребра
Цилиндр имеет две круглые поверхности и одну изогнутую поверхность. Круглые грани конгруэнтны (одинаковы по размеру и форме) и расположены на каждом конце цилиндра. Изогнутая поверхность соединяет две круглые грани и имеет форму прямоугольника, свернутого в трубку.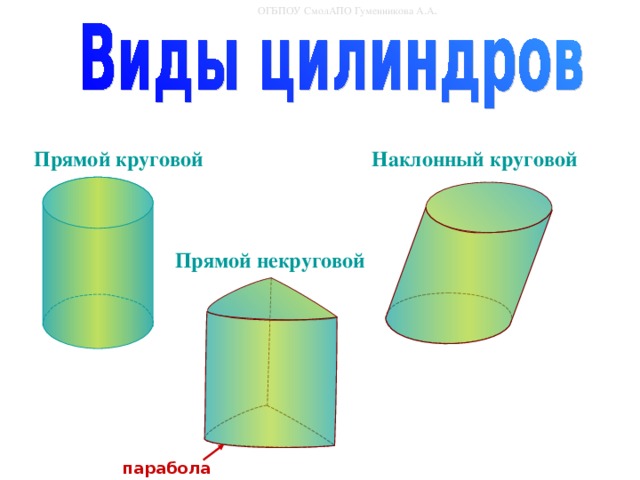 Посмотрим, сколько граней, вершин и ребер у цилиндра:
Посмотрим, сколько граней, вершин и ребер у цилиндра:
- Грани: Цилиндр имеет всего 3 грани (2 плоские круглые грани + 1 изогнутая грань)
- Кромки: Цилиндр имеет 2 кромки (одну вверху и одну внизу)
- Вершины: Цилиндр имеет 0 вершин (поскольку два края цилиндра нигде не пересекаются)
Типы цилиндров
Мы только что прочитали о некоторых реальных примерах цилиндра, которые показывают, что он может быть разных типов. В геометрии есть четыре различных типа цилиндров. Они следующие:
- Прямой круговой цилиндр: Если оси двух параллельных оснований перпендикулярны центру основания, такой цилиндр называется правильным круговым. Пример: банка газировки.
- Наклонный цилиндр: Наклонный цилиндр — это цилиндр, стороны которого опираются на основание. При этом стороны не перпендикулярны центру основания.
 Пример: Пизанская башня.
Пример: Пизанская башня. - Эллиптический цилиндр: Цилиндр, основание которого имеет форму эллипса, называется эллиптическим цилиндром. Пример: оптическая линза.
- Правый круговой полый цилиндр или цилиндрическая оболочка: Состоит из двух правильных круговых цилиндров, заключенных один внутри другого. Точка оси общая и перпендикулярна центральному основанию. Он отличается от правильного круглого цилиндра тем, что он полый по своей природе, то есть внутри есть некоторое пространство или пустота. Пример: Гидравлические цилиндры.
Посмотрите на изображение ниже, чтобы получить обзор всех четырех типов цилиндров, описанных выше.
Свойства цилиндра
Каждая геометрическая фигура имеет свои характеристики или некоторые свойства, отличные от других фигур. Точно так же давайте изучим некоторые свойства формы цилиндра, перечисленные ниже:
- Цилиндр имеет одну изогнутую поверхность и две одинаковые плоские грани.

- Два круглых основания конгруэнтны друг другу.
- Его размер зависит от радиуса основания и высоты криволинейной поверхности.
- В отличие от конуса, куба или прямоугольного параллелепипеда, цилиндр не имеет вершины. Это означает, что в цилиндре нет определенного угла.
- Основание и вершина цилиндра идентичны, т.е. у него одно и то же основание — либо круглое, либо эллиптическое.
Формулы цилиндра
Каждая трехмерная геометрическая фигура имеет как минимум две основные формулы: площадь поверхности и объем. Точно так же цилиндр имеет три основные формулы, связанные с его площадью поверхности и объемом.
- Площадь боковой поверхности (LSA) или площадь криволинейной поверхности (CSA) цилиндра = 2πrh
- Общая площадь поверхности цилиндра = 2πr(h+r)
- Объем цилиндра = πr 2 ч
Во всех этих формулах ‘r’ представляет собой радиус основания, а ‘h’ представляет собой высоту цилиндра.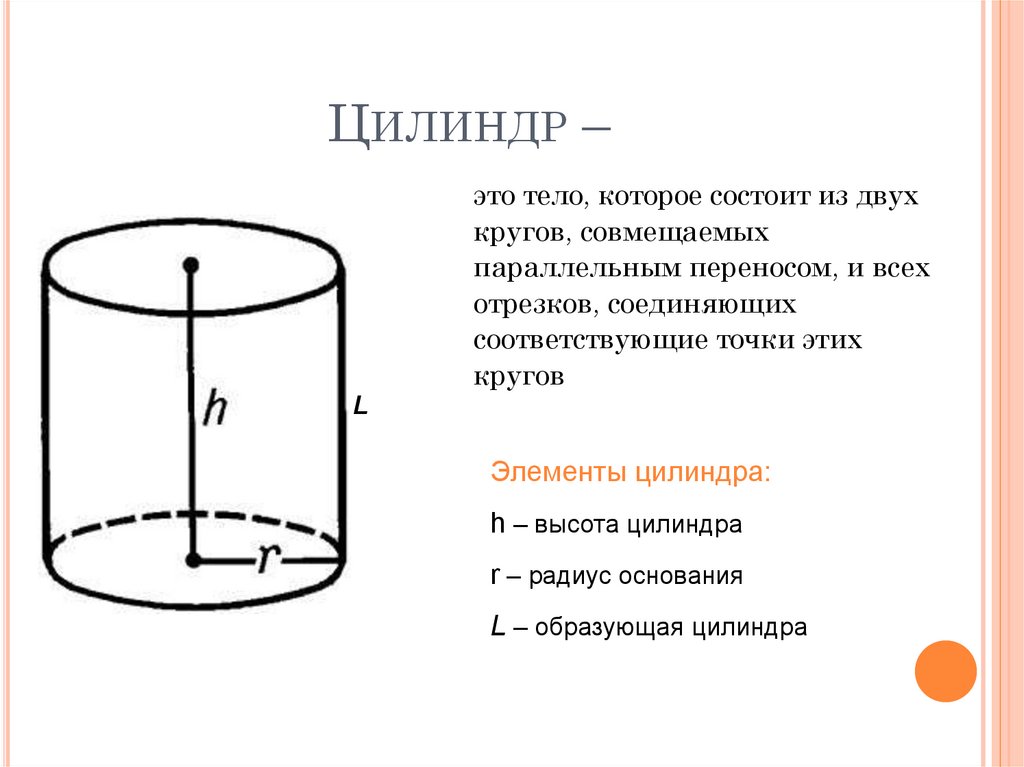
Давайте подробно узнаем о приведенных выше формулах цилиндров.
Площадь криволинейной поверхности цилиндра:
Площадь криволинейной поверхности также называется площадью боковой поверхности. Площадь, образованная криволинейной поверхностью цилиндра, т. е. пространство, занимаемое между двумя параллельными круглыми основаниями, известна как его ППС. Формула для площади криволинейной поверхности цилиндра имеет следующий вид:
Площадь криволинейной поверхности (CSA) = 2πrh квадратных единиц
(Примечание: «h» — высота, «r» — радиус, а значение π равно 22/7 или приблизительно 3,14).
Это потому, что, когда изогнутая грань цилиндра развернута, мы получаем прямоугольник, длина которого = длина окружности круга = 2πr, а ширина = высота цилиндра = h. Таким образом, его площадь равна: длина × ширина = 2πr × h.
Общая площадь поверхности цилиндра:
Общая площадь поверхности определяет общую площадь, которую он занимает, включая основания. Цилиндр состоит из двух кругов и одного изогнутого листа. Итак, чтобы узнать общую площадь поверхности цилиндра, мы вычисляем площадь криволинейной поверхности и площадь двух кругов.
Цилиндр состоит из двух кругов и одного изогнутого листа. Итак, чтобы узнать общую площадь поверхности цилиндра, мы вычисляем площадь криволинейной поверхности и площадь двух кругов.
Площадь криволинейной поверхности (CSA) = длина окружности × высота
CSA = 2πr × h
Площадь круга = πr 2
Общая площадь поверхности (TSA) = площадь криволинейной поверхности + 2 (площадь круга)
Общая площадь поверхности (TSA) = 2πrh + 2πr 2 = 2πr(h+r) квадратных единиц
(Примечание: «h» — высота, а «r» — радиус. Есть две окружности, поэтому мы умножаем площадь основания круга на 2)
Объем цилиндра:
Объем цилиндра определяет плотность или объем занимаемого им пространства. Если мы хотим, чтобы цилиндр наполнился водой, то необходимое количество воды можно рассчитать, найдя его объем.
Объем цилиндра = Площадь круга × высота
Объем = πr 2 × h
Объем цилиндра, V = πr 2 h кубических единиц
где ‘h’ высота, а «r» — радиус.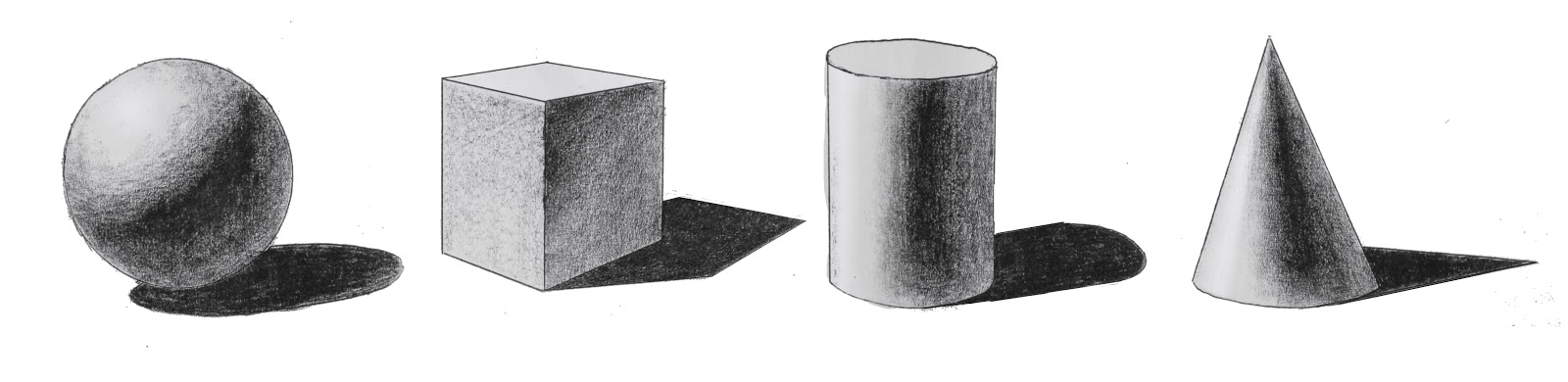
Цилиндрическая сетка
Цилиндрическая сетка представляет собой двухмерную структуру, созданную путем ее развертывания. Это помогает нам визуализировать форму цилиндра и площадь его поверхности. Когда мы разворачиваем цилиндр, мы получаем прямоугольник, соединенный двумя одинаковыми окружностями, которые образуют верхнее и нижнее основания цилиндрической формы. Посмотрите на изображение сетки цилиндра, показанное ниже.
☛ Статьи по теме:
Ознакомьтесь со следующими темами, связанными с формой цилиндра.
- Калькулятор цилиндров
- Калькулятор площади поверхности цилиндра
- Калькулятор объема цилиндра
- Калькулятор высоты цилиндра
Часто задаваемые вопросы о цилиндрической форме
Что такое цилиндр?
Цилиндр представляет собой трехмерную фигуру, состоящую из двух круглых оснований, соединенных с изогнутой поверхностью, образованной путем складывания прямоугольника. Верхняя и нижняя грани цилиндра конгруэнтны. Всего у него 3 грани, 2 ребра и нет вершин.
Верхняя и нижняя грани цилиндра конгруэнтны. Всего у него 3 грани, 2 ребра и нет вершин.
Что такое формулы цилиндров?
Три основные формулы цилиндра:
- Общая площадь поверхности = 2πr(r+h) квадратных единиц
- Площадь изогнутой поверхности = 2πrh квадратных единиц
- Объем = πr 2 ч кубических единиц
Каков объем цилиндра?
Объем цилиндра – это занимаемое им пространство. Его можно рассчитать по формуле: V = πr 2 ч кубических единиц.
Что такое площадь поверхности цилиндра?
Цилиндр имеет два основания и изогнутую поверхность. Существует два типа формул площади для формы цилиндра: площадь криволинейной поверхности и общая площадь поверхности. Формулы площади поверхности цилиндра приведены ниже:
- Общая площадь поверхности = 2πr(r+h) квадратных единиц
- Площадь изогнутой поверхности = 2πrh квадратных единиц
Каковы реальные примеры цилиндров?
Реальные примеры цилиндра: рулоны туалетной бумаги, банки, трубы, мензурки и т. д.
д.
Сколько ребер у цилиндра?
Цилиндр имеет 2 грани. Край — это место, где встречаются 2 грани. Край может быть прямым или изогнутым. Например, у куба 12 прямых граней, а у цилиндра 2 изогнутых. Мы знаем, что цилиндр представляет собой комбинацию двух кругов и одного прямоугольника. Два прямых края прямоугольника сгибаются, образуя изогнутые края цилиндра.
Что такое общая площадь поверхности цилиндра?
Общая площадь поверхности цилиндра равна сумме площади криволинейной поверхности и площади двух круглых оснований. Это дается как:
Общая площадь поверхности = площадь изогнутой поверхности + площадь двух круглых оснований
Общая площадь поверхности (TSA) = 2πrh + 2πr 2 = 2πr(h+r) квадратных единиц
Что такое площадь основания цилиндра?
Площадь, занимаемая в пределах границы круглого основания цилиндра, называется площадью его основания. Единицы площади основания цилиндра всегда выражаются в квадратных сантиметрах, квадратных дюймах, квадратных футах и т. д. В геометрии у нас есть специальная формула для нахождения площади основания цилиндра, равная πr 2 где r — радиус основания.
д. В геометрии у нас есть специальная формула для нахождения площади основания цилиндра, равная πr 2 где r — радиус основания.
Список всех формул цилиндра.
Все формулы, относящиеся к цилиндру радиуса ‘r’ и высоты ‘h’, приведены ниже:
| Площадь основания цилиндра | πr 2 |
|---|---|
| Изогнутая поверхность цилиндра | 2πrh |
| Общая площадь поверхности цилиндра | 2πrh+ 2πrr 2 |
| Объем цилиндра | πr 2 ч |
Каковы свойства цилиндра?
Ниже перечислены некоторые свойства цилиндра:
- Он имеет одну криволинейную поверхность, две изогнутые кромки и две плоские круглые грани.
- Два плоских круглых основания конгруэнтны друг другу.
- Нет вершины.
- Размер цилиндра зависит от радиуса круглого основания и его высоты.

Применима ли формула Эйлера к цилиндру?
Формула Эйлера применима только к трехмерным фигурам с плоскими гранями (т. е. она применима к многогранникам). Таким образом, это НЕ применимо к цилиндру.
Сколько граней у цилиндра?
В цилиндре имеются две плоские круглые поверхности и одна криволинейная поверхность. Таким образом, у него всего 3 лица.
Цилиндр: форма, определение, типы, формулы, свойства
- Автор
Мадхурима Дас - Последнее изменение 16-01-2023
Из повседневной жизни мы знаем несколько вещей цилиндрической формы. Цилиндр или цилиндрическая конструкция традиционно рассматривается как трехмерное тело в форме призмы с кругом в основании. Это одна из самых простых криволинейных геометрических фигур. Этот традиционный взгляд до сих пор полезен при решении элементарных геометрических задач. Но передовая математическая точка зрения состоит в том, что цилиндрическая поверхность — это бесконечная криволинейная поверхность.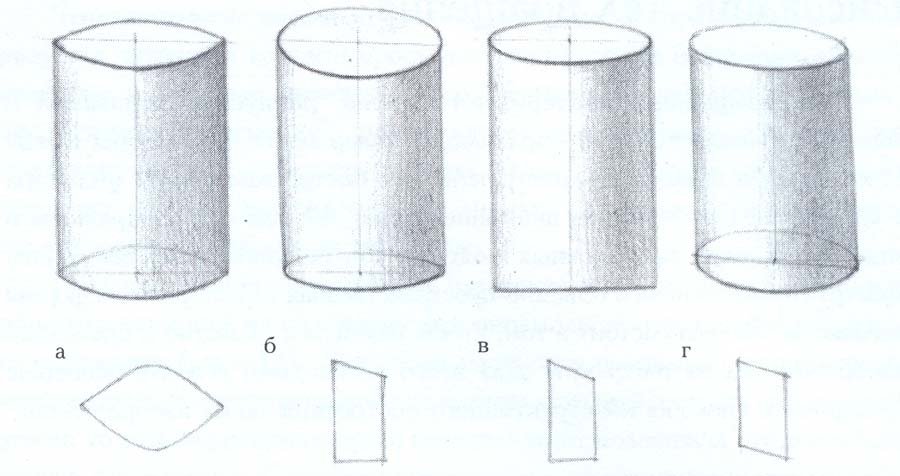 Это определение в настоящее время используется в различных современных разделах геометрии и топологии. В этой статье мы поговорим о характеристиках, типах цилиндров и некоторых формулах, связанных с цилиндрическими конструкциями.
Это определение в настоящее время используется в различных современных разделах геометрии и топологии. В этой статье мы поговорим о характеристиках, типах цилиндров и некоторых формулах, связанных с цилиндрическими конструкциями.
Кроме того, мы предоставили несколько решенных примеров общих математических формул, касающихся площади и объема цилиндров. Приведенные здесь определения и решенные примеры предназначены для того, чтобы помочь учащимся 8, 9 и 10 классов лучше понять цилиндрические фигуры. Читайте дальше, чтобы узнать больше о цилиндрических фигурах.
Цилиндр — это основной трехмерный геометрический объект с одной изогнутой поверхностью, известной как боковая поверхность, и двумя круглыми поверхностями на концах. Цилиндр имеет три грани, два ребра (где встречаются две грани) и НЕТ вершин (углы, где встречаются два ребра), поскольку у него нет углов.
Свойства цилиндра
Цилиндр обладает некоторыми уникальными свойствами.
- Цилиндрическая конструкция имеет боковую поверхность и два основания.
 Общая площадь поверхности равна сумме площади боковой поверхности и двух оснований.
Общая площадь поверхности равна сумме площади боковой поверхности и двух оснований. - Основания параллельны и идентичны.
- Это похоже на призму, поскольку везде имеет одинаковое поперечное сечение.
- Цилиндр может иметь два типа оснований: эллиптическое и круглое.
Типы цилиндров
Есть четыре типа цилиндрических структур, которые можно найти вокруг.
Посмотрим, как они выглядят.
- Прямоугольные цилиндрические конструкции
- Наклонные цилиндрические конструкции
- Эллиптические цилиндрические конструкции
- Цилиндрические оболочковые или полые цилиндрические конструкции
Прямоугольный цилиндр
Прямоугольный цилиндр представляет собой объект, образованный вращением прямоугольника по одной из сторон как ось.
Если ось (одна из сторон прямоугольника) перпендикулярна радиусу \(\left( r \right),\), то цилиндр называется прямым круговым цилиндром.
Основание и вершина цилиндра круглые и параллельны друг другу, расстояние между этими круглыми гранями цилиндра называется высотой \(\left( h \right),\) цилиндра.![]()
Наклонный цилиндр
Если круглые грани расположены не друг над другом, а сбоку, а ось образует угол, отличный от прямого угла к основаниям, то такой цилиндр называется наклонным.
Эллиптический цилиндр
Цилиндр с основаниями эллиптической формы известен как эллиптическая цилиндрическая конструкция.
Цилиндрическая оболочка или полый цилиндр
Полый цилиндр — это цилиндрическая конструкция, пустая изнутри и имеющая различие радиусов внешней и внутренней поверхности цилиндра. Он может иметь разные площади внутренней боковой поверхности и площади внешней боковой поверхности, поскольку внутренний и внешний радиусы не совпадают.
Некоторые примеры полых цилиндров:
Примеры объектов цилиндрической формы
Батарея, железный стержень, деревянная палка для людей, свечи, бутылка с водой и газовый баллон — вот несколько примеров цилиндрической формы.
Какова площадь цилиндра?
Пространство, занимаемое плоской формой или поверхностью объекта, называется площадью. Площадь фигуры — это количество единичных квадратов, охватывающих поверхность замкнутой фигуры. Мы можем измерить площадь в квадратных единицах, таких как квадратные сантиметры, квадратные дюймы, квадратные футы и т. д.
Площадь фигуры — это количество единичных квадратов, охватывающих поверхность замкнутой фигуры. Мы можем измерить площадь в квадратных единицах, таких как квадратные сантиметры, квадратные дюймы, квадратные футы и т. д.
Формула площади цилиндра
Площадь цилиндра — это общее пространство, занимаемое цилиндром в трехмерной геометрии. Площадь цилиндра равна сумме площадей боковой поверхности и площадей двух круговых оснований. Между двумя круглыми основаниями имеется изогнутая или боковая поверхность. Когда изогнутая поверхность открыта, она выступает за прямоугольную фигуру. Для определения площади цилиндра используются различные факторы: высота, радиус, ось, сторона и основание. Радиус цилиндра считается радиусом двух круговых граней. Радиус цилиндра можно представить как \(\left(r\right)\), а перпендикулярное расстояние между двумя круглыми гранями известно как высота цилиндра. Высота цилиндра определяется как \(\left(h\right)\)
Площадь поверхности цилиндрической конструкции можно разделить на две части.
- Площадь криволинейной поверхности (CSA)
- Общая площадь поверхности (TSA)
Площадь криволинейной поверхности цилиндра
Площадь криволинейной поверхности также известна как площадь боковой поверхности. Площадь криволинейной поверхности означает площадь цилиндрической конструкции без площади круглого основания.
Обычно площадь измеряется в квадратных единицах, таких как квадратный сантиметр, квадратный метр и т. д.
Если вскрыть искривленный участок поверхности цилиндра, то обнаруживается прямоугольная форма.
Область криволинейной поверхности включает два круговых ребра, которые могут совпадать с длиной окружности круга.
Формула длины окружности равна \(2\pi r.\)
Итак, можно сказать, что длина прямоугольника (после раскрытия криволинейной поверхности) равна \(2\pi r\), а ширина равно \(\left( h \right),\)
Следовательно, площадь криволинейной поверхности равна \(2\pi r \times h = 2\pi rh\) (поскольку площадь прямоугольника равна длине \( \times\) ширина или \(l \times b\)).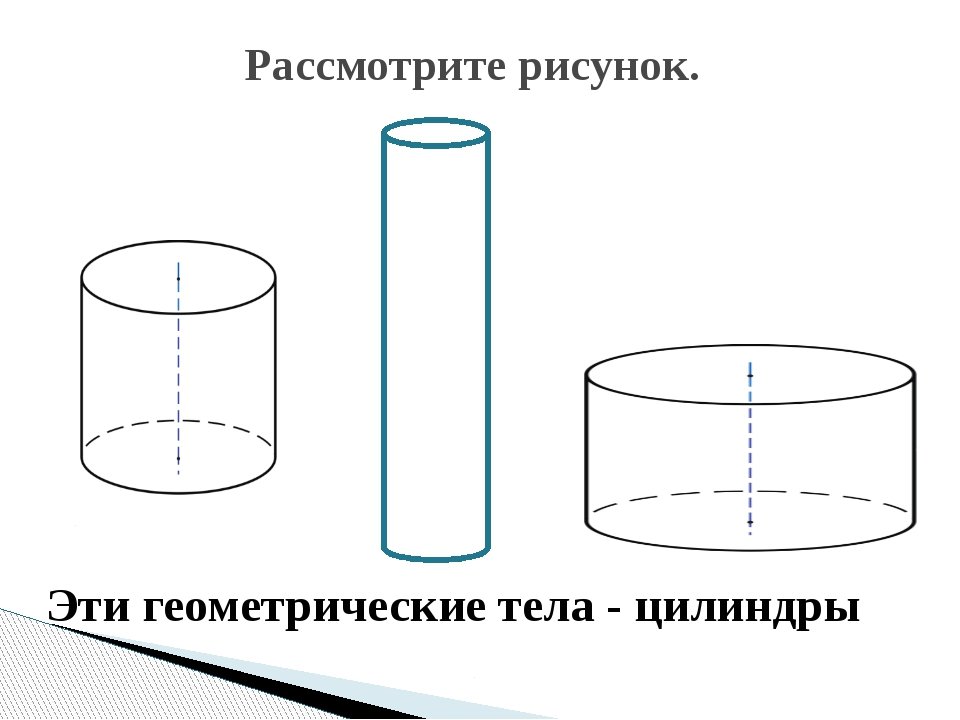 92}\)]
92}\)]
Каков объем цилиндра?
Объем — это пространство, занимаемое веществом (твердым, жидким, газообразным или плазменным) внутри трехмерного объекта, или объем трехмерного объекта обычно определяется как емкость объекта, которая может удерживать вещество.
Например:
- Песок в цилиндрической емкости.
- Вода в цилиндрическом баке.
- Газ в цилиндрической емкости.
- Как правило, объем измеряется в кубических метрах или кубических сантиметрах, а для жидкости используется литр.
Объем цилиндра: Формула
Цилиндрическая структура представляет собой трехмерное твердое тело. В общем случае объем трехмерной фигуры является произведением ее площади основания и высоты.
Объем цилиндрической конструкции равен произведению площади круглого основания на высоту цилиндра.
Объем цилиндра измеряется в кубических единицах. 92} h. \)
Решенные примеры
Вопрос 1: Радиус цилиндрической структуры — \ (5 \, {\ Text {Cm}}}}}}}} \ (5 \, {\ {CM}}}}}}}}}}}}}}}}}}}}}}}}}}}}) \ (5 \) \ (\ text {cm}} \. 2}{\text{h}}\) кубических единиц . 92} \times 20\)
2}{\text{h}}\) кубических единиц . 92} \times 20\)
\(r = \sqrt {15,92\,} \, = 3,99 \приблизительно 4\,{\text{m}}\)
Следовательно, радиус резервуара равен \(4\ ,{\text{м}}\) (приблизительно).
Вопрос 5: Найдите объем цилиндрической металлической трубы, длина которой \(40\,{\text{см}}\) , а внешний радиус равен \(80\,{\ text{cm,}}\) и толщина металлической трубы \(2\,{\text{cm}}{\text{.}}\) Используйте \(\pi = 3.14\)
Ответ: Дано 93}.\)
Резюме
Цилиндрическая структура имеет одну криволинейную поверхность и два основания, нулевую вершину и два ребра. Это призма с двумя основаниями. Их формы можно разделить на четыре типа; это правильный круговой цилиндр, эллиптический цилиндр, наклонный цилиндр и полые цилиндрические структуры. Два основания цилиндрической конструкции параллельны друг другу, и разница между двумя основаниями называется высотой или высотой.
Часто задаваемые вопросы о цилиндрах
Ниже приведены ответы на наиболее часто задаваемые вопросы о цилиндрических конструкциях:
| Вопрос 1: Каково использование цилиндрической конструкции s ? Ответ: Цилиндрические конструкции используются в основном для контейнеров, таких как свечи, батареи, железные стержни и т.  д. Полые цилиндры широко используются в повседневной жизни, такие как соломинки, трубки, трубки, мензурки и т. д. д. Полые цилиндры широко используются в повседневной жизни, такие как соломинки, трубки, трубки, мензурки и т. д. |
| Вопрос 2: Что такое цилиндр и каковы его свойства? Ответ: Цилиндрическая конструкция имеет два основания и одну изогнутую поверхность. Основания цилиндрической конструкции конгруэнтны и параллельны и лежат точно друг над другом. Цилиндр может иметь два типа оснований: эллиптическое и круглое. |
| Вопрос 3: Что такое цилиндрическая форма? Ответ: Цилиндрическую форму можно найти в различных вещах вокруг нас, таких как газовый баллон для приготовления пищи, железный стержень, свеча и так далее. Эта форма имеет два параллельных основания и одну боковую поверхность. |
| Вопрос 4: Какие бывают типы цилиндров? Ответ: Существует четыре типа цилиндров: прямой круговой цилиндр, наклонный цилиндр, эллиптический цилиндр и полый цилиндр. 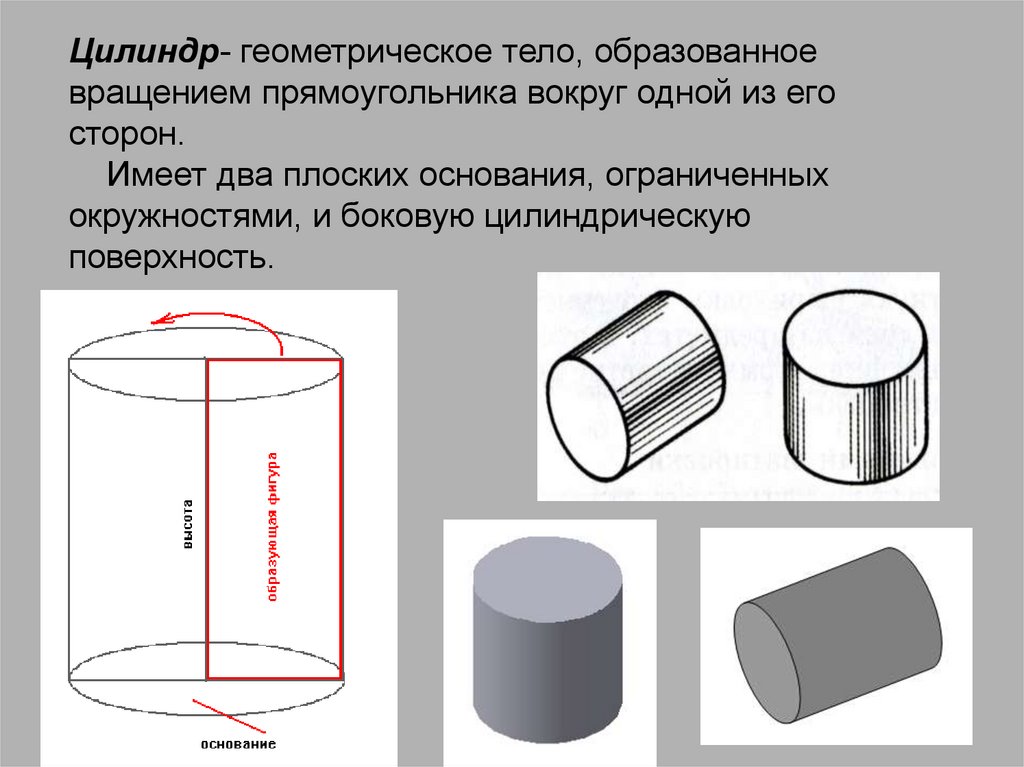
|


 Пример: Пизанская башня.
Пример: Пизанская башня.

 Общая площадь поверхности равна сумме площади боковой поверхности и двух оснований.
Общая площадь поверхности равна сумме площади боковой поверхности и двух оснований.