Содержание
Как определить размер бисера
При
работе с
бисером рано или поздно возникает вопрос, как правильно
определять его величину. Если в самом начале творческого пути это не
столь важно (для первых работ сгодится практический любой вариант), то
далее проблема встает ребром.
Бисер продают в целлофановых пакетиках,врассыпную, в тубах или связках. И мы не всегда знаем, какие размеры
есть у нас в запасе – бисер зачастую хранится в различных емкостях, без
маркировки и точного обозначения размера.
Какие существуют эффективные методы вычисления его размеров?
История вопроса и богемская система
В
давние века в Богемии (Чехия) была создана система, с помощью которой
стало возможным стандартизировать размер стеклянных шариков. При отсутствии промышленного производства соблюдать точные величины было
сложно – тогда выдув бисеринок из стекла являлся наполовину ремеслом,наполовину искусством. Те, кто стремился к созданию идеальных
произведений бисероплетения, выкупали у мастеров целые партии, чтобы
получить однородный размер и цвет.
Сейчас
производить стандартизированный
бисер стало гораздо проще. Пальму
первенства в этом ремесле взяла Япония – она усовершенствовала
классические методы производства и создала материал, с помощью которого
делать тканные и вязаные работы из бисера стало удобнее в разы.
Важно!
Бисеринки одинакового размера, созданные при помощи разных технологий,будут отличаться по своему реальному размеру и диаметру!
Чешская
система маркирует
бисер особыми знаками – 5/о, 8/о, 12/о, 13/о и так
далее. Что это означает? Многие считают, что такое обозначение является
отношением размера исходной бусинки к некому эталону, начальной
идеальной бусине размера «о». Маркер 6/о означает, что бисеринка меньше
эталона в 6 раз, 12/о – диаметр бисера меньше эталона в 12 раз. К
современным изделиям эта система применима с натяжкой, потому что она не
годится для всего бисера, представленного на рынке.
Современные способы
Сейчас
используют способ вычисления размера по количеству бисеринок, которое
способно уместиться на нити размером 1 дюйм (2,54 см) или на таком же
отрезке линейки.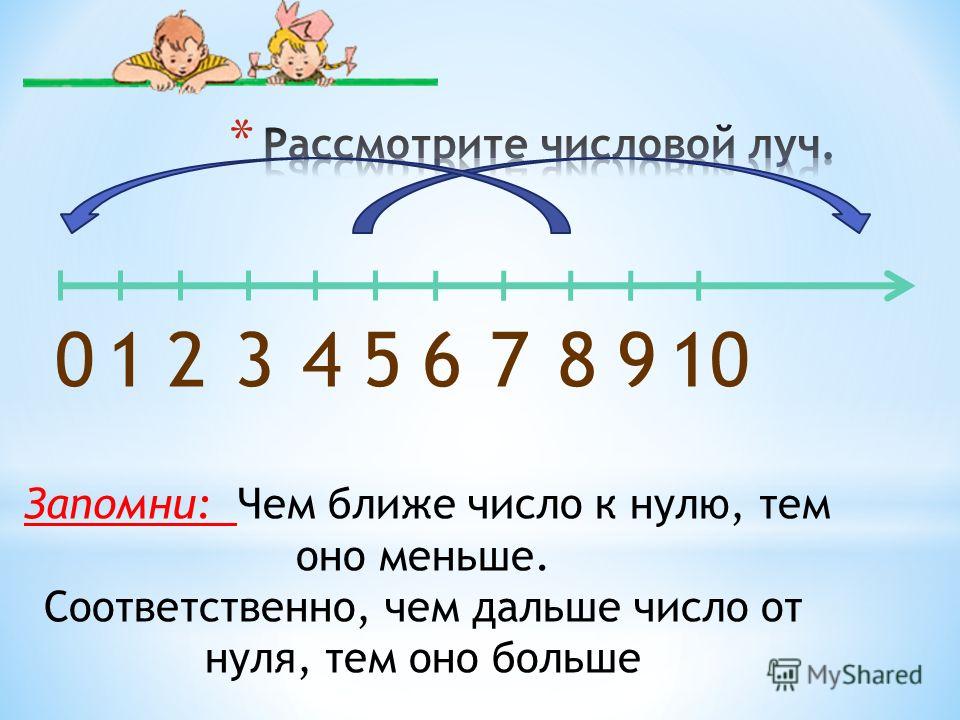 К примеру, бисер 8/о довольно крупный, в 1 дюйм его
К примеру, бисер 8/о довольно крупный, в 1 дюйм его
войдет 8 штук. А вот бисер 20/о мелкий, на 2,54 см линейки уместится
целых 20 штук.
Важно!
Вычислять номер бисера следует по диаметру, т.е. располагать его на
линейке надо центральным отверстием вверх! Ни в коме случае не боковой
стороной.
Существуют
специальные таблицы соответствия чешских размеров бисера их диаметру.
Приведем одну из них. В ней представлены самые распространенные номера и
примерно количество бисера в каждом грамме или на нитке определенной
длины.
Размер бисера | Диаметр бисера, мм | Количество в 1гр | Количество в нитке длиной 1 см | Количество на нитке длиной в 1 дюйм (2,24 см) |
6/о | 4 | 15 | 4 | 10 |
8/о | 3,1 | 38 | 5 | 13 |
10/о | 2,3 | 60 | 6 | 16 |
11/о | 2,1 | 110 | 7 | 18 |
12/о | 1,9 | 190 | 7,5 | 20 |
13/о | 1,7 | 225 | 8 | 21 |
14/о | 1,6 | 260 | 9 | 23 |
15/о | 1,5 | 290 | 10 | 24 |
В
таблице приведены самые распространенные размеры. Величина и вес бисера
Величина и вес бисера
у различных производителей могут существенно отличаться. Здесь представлен лишь главный принцип.
Всегда ли обозначение соответствует реальным размерам?
Сейчас
все производство бисера сосредоточено всего в нескольких странах – Чехии, Тайване, Японии, Китае, Индии и, отчасти, в России. К сожалению, общей для
всех стран шкалы определения величины бисера не выработано, поэтому
каждая фирма ориентируется на собственные традиции и правила. В
результате получается значительный разброс в размерах, отчего начинающим
мастерам бисероплетения сориентироваться сложно.
Важно!
Приведенный выше способ подсчета количества бисера на дюйм не всегда
работает идеально, и цифровое обозначение бисера из Европы не всегда
соответствует такому же обозначению азиатского аналога.
Точнее
всего получается вычислять размер
японского и чешского бисера и
бисеринок, он достаточно стандартизирован, а поэтому стоит дорого. Тайваньский или
Тайваньский или
китайский бисер дешев и хорош для начинающих, но
величина горошин в одном и том же пакетике может существенно отличаться.
А прозрачный бисер 8/о будет значительно больше цветного варианта. При
заказе такого бисера через интернет никогда нельзя быть уверенным, что
получишь именно нужный размер.
Перед
заказом бисеринок в интернет-магазинах важно заранее уточнить размеры.
Обычно в каталоге есть их фотографии на фоне линейки, но нелишним будет
проконсультироваться с менеджером по реальным размерам. Китайский и
тайваньский бисер лучше покупать большими партиями, иначе в следующем
пакетике есть риск получить совсем не тот материал, с которого вы
начинали работу.
Буквенные коды бисера – способ облегчить выбор бисера
Чтобы
облегчить выбор бисера для работы, некоторые западные интернет-магазины
используют особые буквенные коды для его маркировки. Это позволяет
привести к единому знаменателю величину бисера из Японии, Чехии и Китая.
- CROW-BEADS
(очень крупный). Бисеринки небольшого размера от 4 до 10 мм – размеры
Бисеринки небольшого размера от 4 до 10 мм – размеры
от 6/0 и больше. Такой бисер больше похож на бусины. Считается, что
бусинами является тот бисер, чей диаметр превышает 4,5 мм. Широко
применяется для украшения одежды и обуви, создания бижутерии и
сувениров. - E-BEADS (крупный бисер). Бисер с размером от 2,5 до 4
мм – от 8/о до 6/о. Применяется повсеместно – для плетения икон,вышивки, создания украшений. - PONY-BEADS (средний). Иногда
совпадает с бисером E-BEADS, но чаще находится в пределах от 10/о до
8/о. Этот бисер более округлый, с тонким отверстием для нити.
Используется для создания ровного слоя бисера, для качественной вышивки
панно и одежды. - SEED-BEADS (мелкий). Размеры от 15/о до 10/о –
от 1,3 до 3,3 мм. Гладкий округлый материал с тонким отверстием для
нити, идеально подходит для вышивки и декорирования одежды.
Каковы
бы ни были размеры бисера, он открывает мастерам и новичкам
безграничные возможности для творчества, позволяя создавать и
любительские поделки, и настоящие произведения искусства. Если научиться
Если научиться
правильно выбирать материал, то создавать украшения из бисера станет
проще и комфортнее, изделие будет получаться более красивым и ровным.
Желаем Вам удачи в этом нелегком, но крайне интересном занятии!
Натуральные числа: определение, примеры, свойства
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
| Особенности натуральных чисел |
|---|
|
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Ноль предметов значит — ни одного.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
0 и 15;
20 и 50;
100 и 130?
Равно, меньше и больше символов
lo1kvxu-Dc8
Помимо знакомого знака равенства (=), также очень полезно показывать, если что-то не равно (≠) больше, чем
(>) или менее (<)
Это важные знаки, которые нужно знать :
| = | Когда два значения равны | пример: 2+2 = 4 |
| ≠ | Когда два значения определенно , а не равны | пример: 2+2 ≠ 9 |
| < | Когда одно значение меньше другого | пример: 3 < 5 |
| > | Когда одно значение больше другого | пример: 9 > 6 |
Меньше и больше
Знак «меньше» и «больше» выглядят как буква «V» сбоку, не так ли?
Чтобы запомнить, в какую сторону идут знаки «<" и ">«, просто запомните:
- БОЛЬШОЙ > маленький
- маленький < БОЛЬШОЙ
«Маленький» конец всегда указывает на меньшее число, например:
Символ «больше чем»: БОЛЬШОЙ > маленький
Пример:
10> 5
«10 — больше, чем 5″
или в другом месте, около
5 <10
«5 — Менее 10″
9000 «0102
Видите, как символ «указывает» на меньшее значение?
.
 .. или равно …
.. или равно …
Иногда мы знаем, что значение меньше, но также может быть равно !
Например, кувшин может вместить до 4 чашек воды.
Так сколько в нем воды?
Это может быть 4 чашки или меньше 4 чашек: Итак, пока мы не измерим это, все, что мы можем сказать, это «меньше или равно » 4 чашки.
Чтобы показать это, мы добавим дополнительную строку внизу символа «меньше» или «больше», например:
Знак «меньше или равно «: | ≤ | |
Знак «больше или равно «: | ≥ |
Все символы
Вот сводка всех символов:
Символ | Слова | Пример использования |
|---|---|---|
= | равно | 1 + 1 = 2 |
≠ | не равно | 1 + 1 ≠ 1 |
> | больше | 5 > 2 |
< | меньше | 7 < 9 |
≥ | больше или равно | шариков ≥ 1 |
≤ | меньше или равно | собаки ≤ 3 |
Зачем их использовать?
Потому что есть вещи, которые мы не знаем точно . ..
..
… но может еще сказать что-то о .
Итак, у нас есть способы сказать, что мы знаем (что может быть полезно!)
Пример: У Джона было 10 шариков, но он потерял несколько. Сколько у него сейчас?
Ответ: У него должно быть менее 10:
Мрамор < 10
Если у Джона все еще есть несколько мрамор, мы также можем сказать, что у него больше, чем ноль Мрамор:
Мрамол > 0 0.
Но если бы мы думали, что Джон мог потерять все своих шариков, мы бы сказали:
Шарики ≥ 0
Другими словами, количество шариков больше или равно нулю.
Объединение
Иногда мы можем сказать две (или более) вещи в одной строке:
Пример: Бекки начинает с 10 долларов, покупает что-то и говорит: «У меня тоже есть сдача». Сколько она потратила?
Ответ: Что-то больше 0 долларов и меньше 10 долларов (но НЕ 0 или 10 долларов):
«Сколько Бекки тратит» > 0 долларов
«Сколько Бекки тратит» < 10 долларов
Это можно записать всего в одну строку:
$0 < "Сколько Бекки тратит" < $10
Это говорит о том, что 0 долларов меньше, чем «Сколько Бекки тратит» (другими словами, «Сколько Бекки тратит» больше, чем 0 долларов), и что Бекки тратит меньше 10 долларов.
Обратите внимание, что «>» было перевернуто на «<», когда мы поставили перед тем, что тратит Бекки. Всегда проверяйте
маленький конец указывает на маленькое значение .
Смена сторон
В предыдущем примере мы видели, что когда мы меняем сторону, мы также переворачиваем символ.
| Это: | Бекки тратит > $0 | (Бекки тратит больше 0 долларов США) | ||
| это то же самое: | $0 < Бекки тратит | (0 долларов меньше, чем тратит Бекки) |
Просто убедитесь, что маленький конец указывает на маленькое значение!
Вот еще один пример использования «≥» и «≤»:
Пример: у Бекки есть 10 долларов, и она идет за покупками.
 Сколько она потратит (без использования кредита)?
Сколько она потратит (без использования кредита)?
Ответ: Что-то больше или, возможно, равное 0 долларов США и меньше или равное 10 долларам:
Расходы Бекки ≥ 0 долларов
Расходы Бекки ≤ 10 долларов
Это можно записать всего в одну строку:
$0 ≤ Бекки тратит ≤ $10
Длинный пример: перерезание веревки
Вот интересный пример, о котором я подумал:
Пример: Сэм разрезает 10-метровую веревку на две части. Какова длина более длинного куска? Какова длина более короткого куска?
Ответ: Обозначим более длинную длину веревки « L «, а более короткую длину « S »
L должна быть больше 0м (иначе это не кусок канат), а также менее 10 м:
L > 0
L < 10
Итак:
0 < L < 10
Это говорит о том, что L (Большая длина веревки) находится между 0 и 10 (но не 90 0 или 03)
То же самое можно сказать и о более короткой длине « S «:
0 < S < 10
Но я сказал, что есть «более короткая» и «более длинная» длина, поэтому мы также знать:
S < L
(Видите, какая аккуратная математика? Вместо того, чтобы говорить, что «меньшая длина меньше, чем большая», мы можем просто написать « S < L »)
Мы можем объединить все это вот так :
0 < S < L < 10
Это говорит о многом:
0 меньше короткой длины, короткая длина меньше длинной длины, длинная длина меньше 10.
Читая «назад» мы также можем увидеть:
10 больше длинной длины, длинная длина больше короткой длины, короткая длина больше 0. «L») и даже 0<10 (которое мы и так знаем) — все в одном выражении.
ТЕПЕРЬ у меня есть еще один трюк. Если бы Сэм очень старался, он мог бы разрезать веревку ТОЧНО пополам, поэтому каждая половина равна 5 м, но мы знаем, что он этого не сделал, потому что мы сказали, что есть «более короткая» и «длинная» длина, поэтому мы также знаем:
S<5
и
L>5
Мы можем поместить это в очень аккуратное выражение здесь:
0 < S < 5 < L < 10
И ЕСЛИ бы мы думали, что две длины МОГУТ быть ровно 5 мы могли бы изменить это на
0 < S ≤ 5 ≤ L < 10
Пример использования алгебры
Хорошо, этот пример может быть сложным, если вы не знаете алгебры, но я подумал, что вам все равно будет интересно его увидеть:
Пример: Чему равно x+3, если мы знаем, что x больше 11?
Если x > 11 , then x+3 > 14
(Представьте, что «x» — это количество человек на вашей вечеринке. Если на вашей вечеринке более 11 человек, и придут еще 3, то сейчас на вашей вечеринке должно быть более 14 человек.)
Если на вашей вечеринке более 11 человек, и придут еще 3, то сейчас на вашей вечеринке должно быть более 14 человек.)
5250, 5251, 5252, 5253, 5254, 5255, 5256, 5257, 5258, 5259
Темы по алгебре: Отрицательные числа
Урок 3: Отрицательные числа
/ru/алгебра-темы/показатели/содержание/
Что такое отрицательные числа?
Отрицательное число — это любое число меньше нуля. Например, -7 — это число, которое равно семи меньше , чем 0.
-7
Может показаться немного странным говорить, что число на меньше , чем 0. В конце концов, мы часто думаем о ноль означает ничего . Например, если в вашей конфетнице осталось 0 кусочков шоколада, у вас нет конфет . Есть ничего не осталось. В этом случае трудно представить себе меньше, чем ничего.
Однако в реальной жизни бывают случаи, когда вы используете числа меньше нуля. Например, вы когда-нибудь были на улице в очень холодный зимний день, когда температура была ниже нуля? Любая температура ниже нуля является отрицательным числом. Например, температура на этом термометре составляет 90 569 -20 90 570 , или двадцать градусов 90 569 ниже 90 570 нуля.
Вы также можете использовать отрицательные числа для более абстрактных идей. Например, в финансах отрицательные числа могут использоваться для обозначения 9.0569 долг . Если я перевыполню свой счет (сниму больше денег, чем у меня есть на самом деле), мой новый банковский баланс будет отрицательным числом . У меня не только не будет денег в банке — у меня на самом деле будет 90 569 меньше 90 570, чем ничего, потому что я должен банку 90 569 денег.
Посмотрите видео ниже, чтобы узнать больше об отрицательных числах.
com/embed/6U1kCOuNpR4?rel=0&showinfo=0″ allowfullscreen=»» frameborder=»0″>
Любое число без знака минус перед ним считается положительным числом , то есть числом, равным 9.0569 больше ноль. Таким образом, в то время как -7 равно отрицательной семерке , 7 равно положительной семерке , или просто семь .
Знакомство с отрицательными числами
Как вы могли заметить, отрицательные числа пишутся тем же символом, что и при вычитании: знаком минус (-). Знак минус не означает, что вы должны думать о числе вроде -4 как вычесть четыре . В конце концов, как бы вы вычесть это?
-4
Нельзя, потому что не из чего вычитать. Мы можем написать -4 само по себе именно потому, что это не означает вычесть 4 . Это означает 90 569 против 90 570 из четырех.
Взгляните на 4 и -4 на числовой прямой:
Числовую прямую можно представить как состоящую из трех частей: положительное направление , отрицательное направление и ноль . Все, что справа от нуля, равно положительному , а все, что слева от нуля, равно отрицательному . Мы думаем о положительных и отрицательных числах как о противоположны , потому что они находятся на противоположных сторонах числовой прямой.
Все, что справа от нуля, равно положительному , а все, что слева от нуля, равно отрицательному . Мы думаем о положительных и отрицательных числах как о противоположны , потому что они находятся на противоположных сторонах числовой прямой.
Еще одна важная вещь, которую нужно знать об отрицательных числах, это то, что они становятся на меньше по мере удаления от 0. На этой числовой прямой чем дальше слева от находится число, тем оно меньше. Таким образом, 1 меньше, чем 3 . -2 меньше 1 , а -7 меньше -2 .
Понимание абсолютного значения
Когда мы говорим об абсолютном значении числа, мы говорим о расстоянии этого числа от 0 на числовой прямой. Помните, мы говорили, что 4 и -4 находятся на одном расстоянии от 0? Это означает, что 4 и -4 имеют одинаковое абсолютное значение. Мы изображаем взятие абсолютного значения числа двумя прямыми вертикальными линиями | | . Например, |-3| = 3. Это читается как «абсолютное значение отрицательного числа три равно трем».
Мы изображаем взятие абсолютного значения числа двумя прямыми вертикальными линиями | | . Например, |-3| = 3. Это читается как «абсолютное значение отрицательного числа три равно трем».
Важно помнить: даже если отрицательные числа получают меньше по мере удаления от 0 их абсолютное значение становится на больше . Например, -10 меньше, чем -6. Однако |-10| больше, чем |-6| потому что -10 имеет большее расстояние от 0, чем -6.
Вычисления с отрицательными числами
Использовать отрицательные числа в арифметике довольно просто. Есть только несколько специальных правил, о которых следует помнить.
Сложение и вычитание отрицательных чисел
Когда вы складываете и вычитаете отрицательные числа, полезно подумать о числовой прямой, по крайней мере, сначала. Давайте посмотрим на эту проблему: 6 — 7 . Хотя 7 больше 6, вы можете вычесть его точно так же, как и любое другое число, если вы понимаете, что есть числа меньше , чем 0.
6 — 7 = -1
Числовая линия позволяет легко представить себе эту проблему, есть также прием, который вы могли бы использовать для ее решения.
Во-первых, не обращайте внимания на отрицательные знаки. Просто найдите разность между двумя числами. В данном случае это означает решение на 7 — 6 , что равно 1. Затем посмотрите на исходную проблему. Какое число имеет наибольшее абсолютное значение ? В данном случае это -7. Поскольку -7 — отрицательное число, наш ответ тоже будет единицей: -1. Поскольку абсолютное значение -7 больше, чем расстояние между 6 и 0 , наш ответ в конечном итоге будет меньше, чем 0 .
Добавление отрицательных чисел
Как бы вы решили эту задачу?
6 + -7
Хотите верьте, хотите нет, но это та же самая проблема, которую мы только что решили!
Это потому, что знак «плюс» просто сообщает вам, что вы объединяете два числа. Когда вы объединяете отрицательное число с положительным, сумма будет на 90 569 меньше, чем на 90 570, чем исходное число, так что вы могли бы также получить 90 569, вычитая 90 570. Итак, 6 + -7 — это то же самое, что 6 — 7 , и оба они равны -1.
Когда вы объединяете отрицательное число с положительным, сумма будет на 90 569 меньше, чем на 90 570, чем исходное число, так что вы могли бы также получить 90 569, вычитая 90 570. Итак, 6 + -7 — это то же самое, что 6 — 7 , и оба они равны -1.
6 + -7 = -1
Всякий раз, когда вы видите положительный и отрицательный знак рядом друг с другом, вы должны читать это как минус . Точно так же, как 6 + -7 равно 6 — 7:
- 10 + -11 равно 10 — 11.
- 3 + -2 равно 3 — 2.
- 50 + -100 равно 50 -100.
Это верно всякий раз, когда вы добавляете отрицательное число. Добавление отрицательного числа всегда равносильно вычитанию абсолютного значения этого числа.
Вычитание отрицательных чисел
Если прибавление отрицательного числа на самом деле равносильно вычитанию, как вы вычесть из отрицательное число? Например, как решить эту проблему?
6 — — 3
Если вы догадались, что добавляете к ним , вы правы. И вот почему: помните, как мы говорили, что отрицательное число противоположно положительному? Мы сравнили их с вами и вашим зеркальным отражением. Ваше зеркальное отражение является вашей противоположностью, что означает, что ваше зеркальное отображение противоположно вам . Другими словами, противоположность вашей противоположности — это , вы .
И вот почему: помните, как мы говорили, что отрицательное число противоположно положительному? Мы сравнили их с вами и вашим зеркальным отражением. Ваше зеркальное отражение является вашей противоположностью, что означает, что ваше зеркальное отображение противоположно вам . Другими словами, противоположность вашей противоположности — это , вы .
Таким же образом вы можете упростить эти два знака минус, прочитав их как два отрицания. Первый минус отрицает — или делает отрицательным — второе. Поскольку отрицательное или противоположное отрицательному значение является положительным, вы можете заменить оба знака минус знаком плюс. Это означает, что вы должны решить это:
6 + 3
Это намного проще решить, верно? Если это кажется запутанным, вы можете просто запомнить этот простой прием: Когда вы видите два знака минуса подряд , замените их знаком плюса .
Итак, 6 минус минус 3 равно 6 плюс 3. Это равно 9. Другими словами, 6 — -3 равно 9.
Это равно 9. Другими словами, 6 — -3 равно 9.
Запоминание всех правил сложения и вычитания чисел может быть непосильным. Посмотрите видео ниже, чтобы узнать, как это сделать.
Умножение и деление отрицательных чисел
Существует два правила умножения и деления чисел:
- Если вы умножаете или делите два числа, которые оба являются положительными или оба отрицательными, ваш результат будет положительным .
- Если вы умножаете или делите положительное число и отрицательное число, ваш результат будет минус .
Вот оно! Вы умножаете или делите как обычно, а затем используете эти правила, чтобы определить, будет ли ответ положительным или отрицательным. Например, возьмем эту задачу: -3 ⋅ -4 . 3 ⋅ 4 равно 12.

 Бисеринки небольшого размера от 4 до 10 мм – размеры
Бисеринки небольшого размера от 4 до 10 мм – размеры Натуральный ряд бесконечен.
Натуральный ряд бесконечен.